整数長ジョブシーケンス問題

概要

N個のジョブがあるとします。 $i\ (1\leq i \leq N)$ 番目のジョブは実行時間に $L_i$ だけ要するとします。これをノード数mのクラスターコンピュータに投げるとき、どのようにジョブスケジュールを割り振れば、クラスターのノードの実行時間の最大を最小にできるでしょうか。

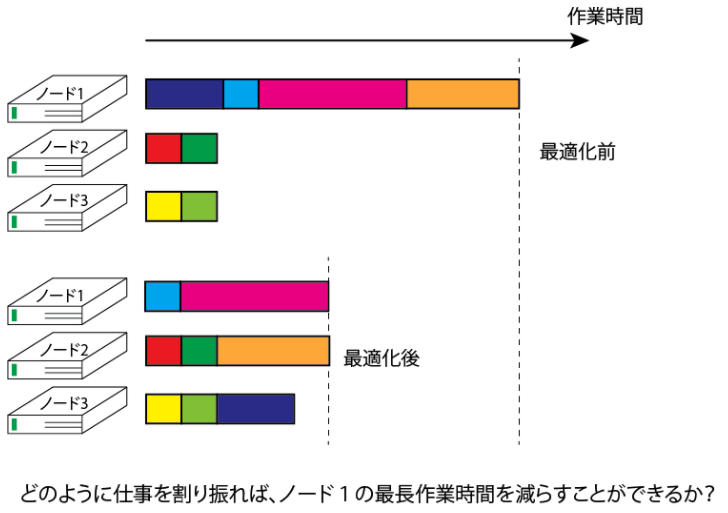
A image of job sequencing with integer length — 整数長ジョブシーケンス問題の概要

概要
直感的な実装数理モデル
Log encodingによる補助変数を用いた(*)式第三項の変更
スクリプト詳解
可視化結果
結言
参考文献
文責

直感的な実装数理モデル

問題の定式化

先ほど概要で説明したことを数式にしましょう。
$\alpha$ ノード番目のジョブの集合を $V_\alpha$ とすると、 $\alpha$ ノード番目の作業時間の合計は

$\displaystyle{ M_\alpha = \sum_{i\in V_\alpha} L_i }$

となります。そして問題は

$\displaystyle{ \min \{\max (M_\alpha) \} }$

となる組合せを探すことになります。ここでジョブの総実行時間が最大となるノードを1としても一般性を失わないため、以降ではノード1の総実行時間を最小化することを考えましょう。ちなみに、この問題はNP困難であることが知られています。

バイナリ変数

最適化に使用するバイナリ変数を、ノード $\alpha$ でジョブ $i$ を行うとき $x_{i, \alpha} = 1$ 、それ以外ならば0と定義します。

また $y_{n, \alpha}$ をノード1とノード $\alpha$ の仕事量の差 $n$ を表す変数とします。具体的には $M_1 - M_\alpha = n \ (\alpha \neq 1, n \geq 0)$ のとき $y_{n, \alpha} = 1$ 、それ以外のとき0と定義します。

それぞれのジョブに対するone-hot encoding

あるジョブ $i$ はいずれか一つのノードで実行されなければなりません。よって

$\displaystyle{ \sum_{\alpha} x_{i, \alpha}= 1 }$

となります。

あるノードでの総実行時間に対するone-hot encoding

$y_{n, \alpha}$ の定義から、ノード $\alpha$ での総実行時間 $\sum_i L_i x_{i, \alpha}$ とノード1の総実行時間 $\sum_i L_i x_{i, 1}$ との差の間に、以下のような関係が成り立たなければなりません。

$\displaystyle{ \sum_{n=0}^{\mathcal{M}} n y_{n, \alpha} = \sum_i L_i (x_{i, 1} - x_{i, \alpha}) }$

ここで $\mathcal{M}$ はユーザが指定する変数で、許容されるノード1とノード $\alpha$ の総実行時間の差を表します。また $y_{n, \alpha}$ に対するone-hot encodingも必要になります。

$\displaystyle{ \sum_{n=0}^\mathcal{M} y_{n, \alpha} = 1 }$

これら制約がないとノード1の総実行時間よりも他のノード $\alpha$ での総実行時間の方が多くなります。

目的関数

最大であるノード1での総実行時間を最小にしたいので、この最適化の目的関数は

$\displaystyle{ \sum_i L_i x_{i, 1} }$

です。

QUBOによる表現

上述の制約及び目的関数をQUBOにすると以下のようになります。

$\displaystyle{ H = \sum_i L_i x_{i, 1} + \lambda_a \sum_{i=1}^N \left( 1-\sum_{\alpha=1}^m x_{i, \alpha} \right)^2 + \lambda_b \sum_{\alpha = 2}^m \left\{ \left( \sum_{n=0}^{\mathcal{M}} n y_{n, \alpha} - \sum_{i=1}^N L_i (x_{i, 1} - x_{i, \alpha}) \right)^2 + \left( 1- \sum_{n=0}^\mathcal{M} y_{n, \alpha} \right)^2 \right\} \tag{*} }$

ここで $\lambda_a, \lambda_b$ はハイパーパラメータです。

Log encodingによる補助変数を用いた(*)式第三項の変更

元の数理モデルは以下のようにノード1とノード $\alpha$ の総実行時間の差が $\mathcal{M}$ 以下であるということ、すなわち

$\displaystyle{ \mathcal{M} \leq \sum_{i=1}^N L_i (x_{i, 1} - x_{i, \alpha}) }$

というものでした。しかしOpenJijチュートリアルのナップサック問題のページにある通り、これのone-hot encodindを考えると制約の数が増え、冗長になります。よってこの問題をLog encodingにより解決しましょう。 $\lfloor a \rfloor$ を $a$ を超えない最大の整数とします。すると(*)式第三項は

$\displaystyle{ \lambda_b \sum_{\alpha = 2}^m \left( \mathcal{M} - \sum_{i=1}^N L_i (x_{i, 1} - x_{i, \alpha}) - \sum_{n=0}^{\lfloor \log_2 (\mathcal{M} -1)\rfloor} 2^n z_n \right)^2 }$

ここで $z_n$ は2進数を表現するために用いた補助のバイナリ変数です。

スクリプト詳解

スクリプト構成

.
├── job_sequencing.py
├── make_energy.py
├── make_instance.py
├── solve_problem.py
└── visualize_solution.py

job_sequencing.py

このスクリプト群のmainスクリプトです。各種関数の呼び出しを行います。

import make_energy as me
import make_instance as mi
import solve_problem as sop
import visualize_solution as vs

if __name__ == '__main__':
    # set problem
    num_nodes, job_length, num_jobs, diff = mi.make_instance()
    # set costs & constraints
    model = me.make_energy(num_nodes=num_nodes, 
                            job_length=job_length, 
                            num_jobs=num_jobs, 
                            diff=diff)
    # set hyper parameters
    parameters = {'h_a': 5.0, 'h_b': 2.0}
    # solve with OpenJij
    solution, broken = sop.solve_problem(model=model, **parameters)
    # check broken 
    print(broken)
    print(solution)
    # visualize result
    vs.visualize_solution(sol_x=solution['x'], 
                            job_length=job_length, 
                            num_nodes=num_nodes)

make_instance.py

問題設定を行います。この問題では以下の定義を行なっています。

num_nodes (int) : 計算ノードの数
job_length (list) : 計算ノードに割り振るジョブの実行時間
diff (int) : ノード0と他のノードの総実行時間の差をどこまで許容するかを示した量

import numpy as np

def make_instance():
    num_nodes = 3
    job_length = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
    num_jobs = len(job_length)
    diff = 3
    return num_nodes, job_length, num_jobs, diff

make_energy.py

解きたい問題のハミルトニアンを計算しています。ここではPyQUBOを用いてバイナリ変数と2進数エンコーディングによる定式化表現を実現しています。

from pyqubo import Array, Constraint, LogEncInteger, Placeholder

def make_energy(num_nodes, job_length, num_jobs, diff):
    # set placeholder
    lambda_a = Placeholder('h_a')
    lambda_b = Placeholder('h_b')
    # set binary variables
    x = Array.create('x', shape=(num_jobs, num_nodes), vartype='BINARY')
    z = LogEncInteger('z', 0, diff)
    # set objective function
    obj = sum([job_length[i]*x[i][0] for i in range(num_jobs)])
    # set one-hot encoding constraint for jobs
    x_const = sum([(1-sum([x[i][a] for a in range(num_nodes)]))**2 for i in range(num_jobs)])
    h_a = Constraint(x_const, label='h_a')
    # set sum of execution time constraint
    y_const = 0
    for a in range(1, num_nodes):
        y_const += (diff-sum([job_length[i]*(x[i][0]-x[i][a]) for i in range(num_jobs)])-z) ** 2
    h_b = Constraint(y_const, label='h_b')
    # compute total energy
    energy = obj + lambda_a * h_a + lambda_b * h_b
    # compile
    model = energy.compile()
    return model

solve_problem.py

OpenJijのシミュレーテッドアニーリングで最適解を求めています。以下のスクリプトのoj.SASamplerをoj.SQASamplerに変更するだけで、ソルバーをシミュレーテッド量子アニーリングに変更することができます。

import openjij as oj

def solve_problem(model, h_a, h_b):
    # set dictionary of hyper parameters
    feed_dict = {'h_a': h_a, 'h_b': h_b, }
    # convert to qubo
    qubo, offset = model.to_qubo(feed_dict=feed_dict)
    # solve with OpenJij (SA)
    num_reads = 100
    sampler = oj.SASampler(num_reads=num_reads)
    response = sampler.sample_qubo(Q=qubo)
    # take mininum state
    dict_solution = response.first.sample
    # decode for analysis
    solution, broken, energy = model.decode_solution(dict_solution, vartype='BINARY', feed_dict=feed_dict)
    return solution, broken

visualize_solution.py

得られた解をmatplotlibで可視化しています。

import math
import matplotlib.pyplot as plt

def visualize_solution(sol_x, job_length, num_nodes):
    exec_time = [0] * num_nodes
    for i in range(len(job_length)):
        for a in range(num_nodes):
            exec_time[a] += sol_x[i][a] * job_length[i]
    yint = range(0, math.ceil(max(exec_time))+1, 2)
    names = ['node '+str(a) for a in range(num_nodes)]
    plt.bar(names, exec_time)
    plt.yticks(yint)
    plt.show()

可視化結果

以下に計算ノードの数は3ノード、ジョブの数を10個とし、それぞれの実行時間を[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]とします。

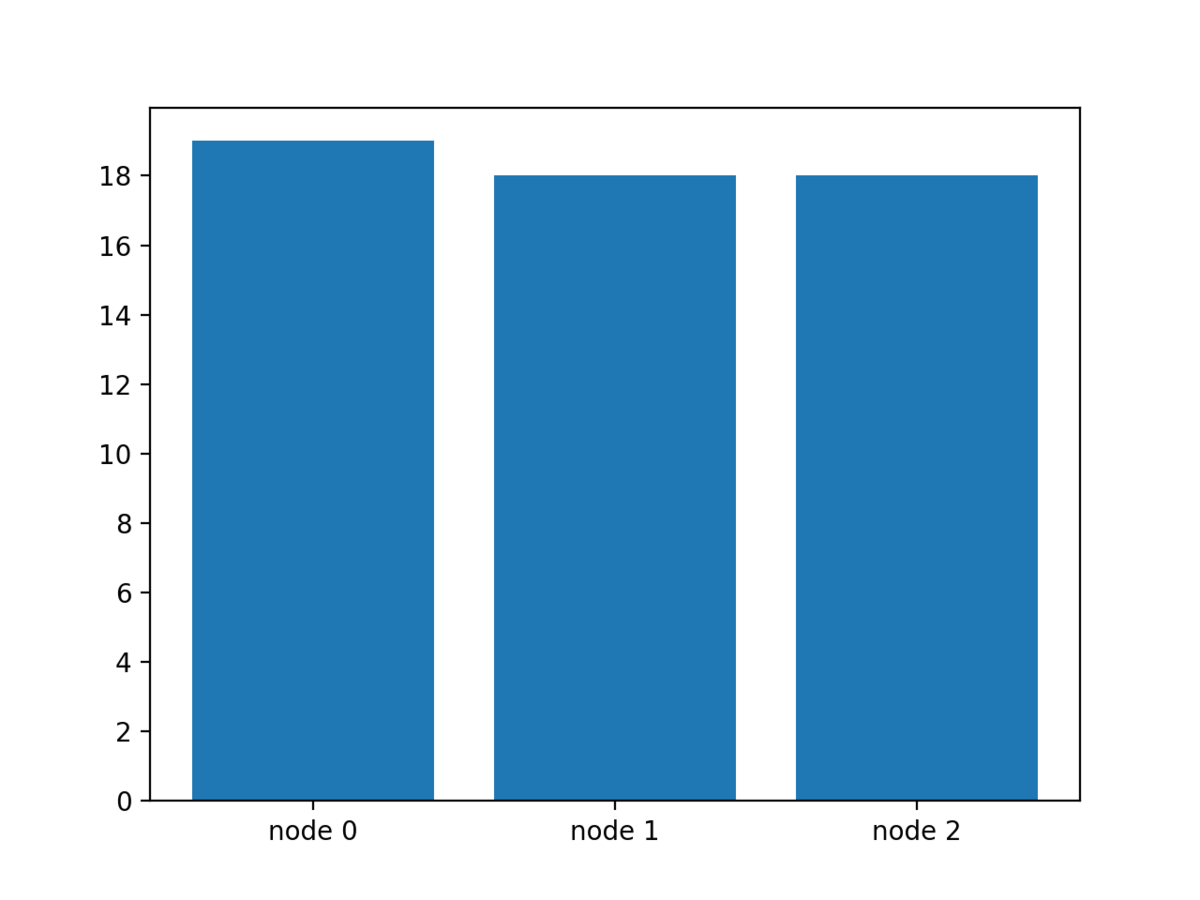
A result image of solution for job sequencing problem — 整数長ジョブシーケンス問題を解いた結果を可視化したもの。

ジョブが3つの計算ノードに分散され、最大であるノード0の実行時間が最小になっていることがわかります。

結言

今回は整数長ジョブスケジューリング問題を解くための、数理モデル・定式化の考え方、そしてOpenJijを用いた実際のスクリプト例をご紹介いたしました。OpenJijチュートリアルではこのほかの問題例も掲載しています。ぜひインストールしてみてください。弊社Jijではこのような最適化問題を軸として、社会の計算困難を解決するべく日々奮闘しています。

参考文献

文責

中村翔、株式会社Jij
Sho K. NAKAMURA, Jij inc.
憂いの篩 -Pensieve-

※ 疑問点や間違いなどございましたら、お気軽にブログ上でご質問ください。

Jij Tech Blog

Jij inc.の開発日記です