Wishart Planted Ensemble (WPE)

はじめに

本記事はJijにてインターンとして勤務してくださっている方が中心となって書いた記事です。

概要

組合せ最適化問題のような難しいとされる問題が与えられたとき、その問題を(近似的にでも)解く手法の開発は言うまでもありませんが非常に重要です。そしてその開発において、それが他と比べてどれくらい優れているのかを把握しておく必要があります。しかし一般に異なるアルゴリズムの性能を比べることは簡単ではありません。分からない問題があるから様々な手法が開発されるのであって、例えば与えられた問題の「真の値」からどれくらい近いかを知ることは一般には不可能だからです。また、答えがあらかじめ分かっている問題を解かせて性能を測ろうとしても、多くの場合その問題は簡単に解けてしまい、差が見えにくくなってしまうこともあり得ます。従って、真の値は知っているが、解くことは難しい問題を作る必要があり、この記事で紹介するWishart Planted Ensemble (WPE)はイジングモデルにおいてまさにそのような問題を生成する手法の一つとなっているため、アニーリングアルゴリズムのベンチマークとして用いることが可能です。

原論文はこちら (https://arxiv.org/abs/1906.00275)にありますので、この記事を閲覧頂いた上でより詳細な内容を知りたい方は参照してみるといいでしょう。

追記 (2020/10/12)

この記事を見つけてくださった原論文の著者であるFiras HamzeさんとHelmut Katzgraberさんからメールで連絡があり、‬この話を二体相互作用から一般の相互作用に拡張した話 (https://arxiv.org/abs/2005.14344)がアップデートとしてあり、

$ pip install chook

でインストールできるとのことなので、是非試してみてください。

問題設定

概要で述べたことをもう少し具体的に定式化してみましょう。

古典スピン系(自由度が $N$ の系)を考え、スピンの総数は $N$ とします。系の次元は任意です。この系に対してplanted solution, すなわち基底状態をこちらで設定したとして、これを $\vec{t}\in \{\pm1\} ^N$ とします。例えば強磁性解

$\vec{t}=\begin{pmatrix}1&1&\cdots&1\end{pmatrix} ^{\mathrm{T}}$

や反強磁性解

$\vec{t}=\begin{pmatrix}1&-1&\cdots&(-1) ^{N-1}\end{pmatrix} ^{\mathrm{T}}$

が考えられるでしょう。しかし解がこれらのようにオーダーしている必要はなく、任意のスピン配置で構いません。Planted solution $\vec{t}$ が与えられたとき、それを基底状態にもつようなハミルトニアン

$\displaystyle H(\vec{s})=-\frac{1}{2}\sum_{i\not=j}J_{ij}s_is_j$

を生成することが目標です。またイジングモデルの時間反転対称性( $s_i\rightarrow-s_i$ でハミルトニアンが不変)より、 $H(\vec{s})$ を解くと $-\vec{t}$ も基底状態となることが分かります。

WPEの構築

まず次のような関数 $G(\vec{s})$ を考えます。

$\displaystyle G(\vec{s})=\frac{1}{2}\vec{s}^{\mathrm{T}}WW^{\mathrm{T}}\vec{s}=\frac{1}{2}\left|W^{\mathrm{T}}\vec{s}\right|^2$

ここで $W$ は $M\times N$ の実行列です。また $M$ 個の列ベクトル $\vec{w} _ i (i=1\sim M)$ を用いて、 $W=\left(\vec{w} _ 1\cdots\vec{w} _ M\right)$ と書けます。任意のスピン配置について $G(\vec{s})\geq0$ となることは明らかでしょう。特に

$\displaystyle W^{\mathrm{T}}\vec{t}=\vec{0}$

となる $\vec{t}$ が存在すれば、 $G(\vec{t})=0$ となってこれが $G(\vec{s})$ の最小値になります。従って、

$\displaystyle H'(\vec{s})=\frac{1}{2N}\vec{s}^{\mathrm{T}}WW^{\mathrm{T}}\vec{s}$

を定義すれば、このハミルトニアンの基底状態は $\vec{s}=\pm\vec{t}$ となります。係数に $1/N$ がついていますが、これはエネルギーを示量的にする、すなわち $N$ に比例するようにするためで、物理学からの要請です。ここで係数と行列をまとめて相互作用を定義しましょう。

$\displaystyle J'=-\frac{1}{N}WW^{\mathrm{T}}$

ハミルトニアンにおけるこの行列の対角成分にあたる部分を見ると $J' _ {ii} s _ is _ i=J' _ {ii}$ となっていることが分かり、これは定数なので元のハミルトニアンから差っ引いてしまいましょう。すなわち新しい相互作用の行列を $J$ を次のように定義します。

$J=J'-\mathrm{diag}\left(J'\right)$

この $J$ を用いて、ハミルトニアンを次のように定義します。

$\displaystyle H(\vec{s})=-\frac{1}{2}\sum _ {i\not=j}J_ {ij} s _ is _ j$

これまでの議論からこのハミルトニアンが $\vec{s}=\pm\vec{t}$ を基底状態に持つことが分かります。従って、任意のスピン配置 $\vec{t}$ について、 $W ^{\mathrm{T}}\vec{t}=\vec{0}$ となるような行列 $W$ を定義できればハミルトニアンがうまく定義されることが分かりました。次にそのような行列をどのように見つけてくるかを考えましょう。これは $\vec{t}$ と直交するような $\vec{w} _ i$ を $M$ 個見つける問題と等価です。イジングモデルでの変数は $s=\pm1$ であること、すなわち $s ^2=1$ であることを使うと、実は簡単に探すことが出来ます。次の行列を定義します。

$\displaystyle \Sigma ^{1/2}=\sqrt{\frac{N}{N-1}}\left(1-\frac{1}{N}\vec{t}\vec{t} ^{\mathrm{T}}\right)$

明らかに対称行列でかつ $\left(\Sigma ^{1/2}\right) ^{\mathrm{T}}\vec{t}=\vec{0}$ であることが分かります。この性質を利用すると次のようにして $\vec{w} _ i$ を生成できます。まず $\vec{z} _ i\leftarrow\mathcal{N}(\vec{0}, I)$ を取ってきます。すなわち各成分独立に正規分布からランダムに実数を選びます。そうすれば $\vec{w} _ i = \Sigma ^{1/2}\vec{z} _ i$ で $\vec{w} _ i$ が定義できます。 $\Sigma ^{1/2}$ の性質から、直交性は明らかでしょう。

ここで定義されたベクトル $\vec{w} _ i$ は $\mathcal{N}\left(0, (\Sigma ^{1/2}) ^2 \right)$ 、すなわち平均がゼロで共分散行列が $\displaystyle (\Sigma ^{1/2}) ^2$ であるような正規分布に従っています。一般にこのような分布をWishart分布と呼び、WPEの名前の由来となっています。なお、以下のpythonコードでハミルトニアンを辞書型で生成できます。

import numpy as np
def wpe_interaction(solution, M):
    n = len(solution)
    sol_arr = [solution]
    tmp_mat = 1 / n * np.dot(np.transpose(sol_arr), sol_arr)
    sigma_mat = np.sqrt(n / (n - 1)) * (np.identity(n) - tmp_mat)
    int_mat = []
    for i in range(M):
        int_mat.append(np.dot(sigma_mat, np.random.randn(n)))
    int_mat = 1 / n * np.dot(np.transpose(int_mat), int_mat)
    int_dict = {(i, j): int_mat[i, j] for i in range(n) for j in range(n)}
    for i in range(n):
        key = (i, i)
        int_dict.pop(key)
    return int_dict

問題の難しさ

これまでの議論から、実際に任意のスピン配置を基底状態に持つイジングモデルが生成できることが分かりました。しかしこのようにして出来た問題が「使える」ためには、簡単に解けてはいけません。そこでここでは問題がどれくらい難しいのかを考えましょう。

直感的な議論

いきなり数学の問題として議論する前に、直感的にどのようなとき問題が難しくなるのかのイメージをつかんでおきましょう。上のように構成されたイジングモデルの基底状態探索は、言い換えると次の問題を解いていることになります：

与えられた行列 $W$ に対して、

$W^{\mathrm{T}}\vec{t}=\vec{0}$

を満たすようなスピン配置 $\vec{t}$ を探す。

明らかにこの問題の難しさは列ベクトル $\vec{w} _ i$ の数、すなわち $M$ に依存することが分かるでしょう。そこで、 $M$ を変えたときに問題の難しさはどのようになるかを考えましょう。まずスピン配置などとは考えず(すなわち $\vec{t}$ の成分が $\pm1$ だけであることを忘れて)、純粋に線形代数の問題として考えてみましょう。その際解空間 $\mathrm{Ker}W ^{\mathrm{T}}$ の大きさは $N-M$ となっていることが分かります。ここではとりあえず $N>M$ の場合を考えています。従って、 $M$ が小さいとき、例えば $M=1$ の時は解空間が非常に大きくなることが分かります。解空間が大きいと基底状態探索は難しくなり、特に $M=1$ の時に最も問題が難しくなりそうですが、実は実機のコンピューター上でWPEを作るうえではそうはなりません。これはコンピュータが完全な実数を実装できないことが原因で、実際には小数点以下どこかで打ち切らないといけませんが、その丸めこみによって多くの状態が基底状態に「見えて」しまいます。すなわち実際の基底状態とは異なる状態のエネルギーと基底状態のエネルギーの差が非常に小さくなってしまうのです。従って実は $M$ が小さいときに基底状態(誤差を許してエネルギー最小となる状態の意味で、厳密な基底状態ではない)を探すことはそこまで難しくありません。

その逆の $M$ が大きい場合を考えましょう。ここで特に $N>M$ を仮定することをしません。相互作用に定数を加えた $\widetilde{J}$ は次のように書けます。

$\displaystyle \widetilde{J}=-\frac{1}{N}WW ^{\mathrm{T}}=-\frac{\alpha}{M}\sum _ {i=1} ^{M}\vec{w} _ i\vec{w} _ i ^{\mathrm{T}}=-\frac{\alpha}{M}\sum _ {i=1} ^M\Sigma ^{1/2}\vec{z} _ i\vec{z} _ i ^{\mathrm{T}}\Sigma ^{1/2}$

ここで $\alpha=M/N$ とします。 $\vec{z} _ i\leftarrow\mathcal{N}\left(\vec{0}, I _ N\right)$ であるので、大数の法則から

$\displaystyle\lim _ {M\rightarrow\infty}\frac{1}{M}\sum _ i ^{M}\vec{z} _ i\vec{z} _ i ^{\mathrm{T}}=\overline{\vec{z}\vec{z} ^{\mathrm{T}}}=I _ N$

(上線は平均を表します)であるので

$\displaystyle\lim _ {M\rightarrow\infty}\widetilde{J}=\left(\Sigma ^{1/2}\right) ^2=\frac{N-1}{N}\left(I _ N-\frac{1}{N}\vec{t}\vec{t} ^{\mathrm{T}}\right)$

となります。従って $M$ を大きくすれば $\vec{t}$ が自明になってゆき、問題が簡単になります。

ここでの議論から、

$M$ が小さいときは低エネルギー状態を探すことは丸め誤差によって簡単になる
$M$ が大きいときは大数の法則から基底状態探索が簡単になる

ことが分かります。従って、エネルギー最小状態を探すという意味では $M$ が小さすぎもせず、大きすぎもしない場合に問題が一番難しくなると考えられます。

定量的な考察

ここでは上の議論をもう少し定量的にしていきたいと思います。ふつうは系が与えられたときに基底状態を知ることが目標なので、ランダムにスピン配置を決めたとき、その状態のエネルギーが $\varepsilon$ となる確率 $p_E(\varepsilon)$ を考えます。簡単のため、基底状態のエネルギーがゼロになるようにしましょう。これはWPEで生成するイジングモデルの相互作用を $J$ ではなく、 $\widetilde{J}$ に取ることに対応しますが、エネルギー値の定数のシフトなので本質的には変わりません。詳しい導出はここでは省くことにして、 $p_E(\varepsilon)$ は次のような結果になります。

$\displaystyle p_E(\epsilon)=\cases{\frac{1}{\Gamma(M/2)}e ^{M/2-\epsilon-1} \text{ for }\epsilon\geq0\cr 0 \text{ else }}$

これをプロットしたものが以下になります。 $M$ が小さいほど低エネルギー状態である確率が大きくなることが分かります。 f:id:jijinc-intern:20200714204409p:plain

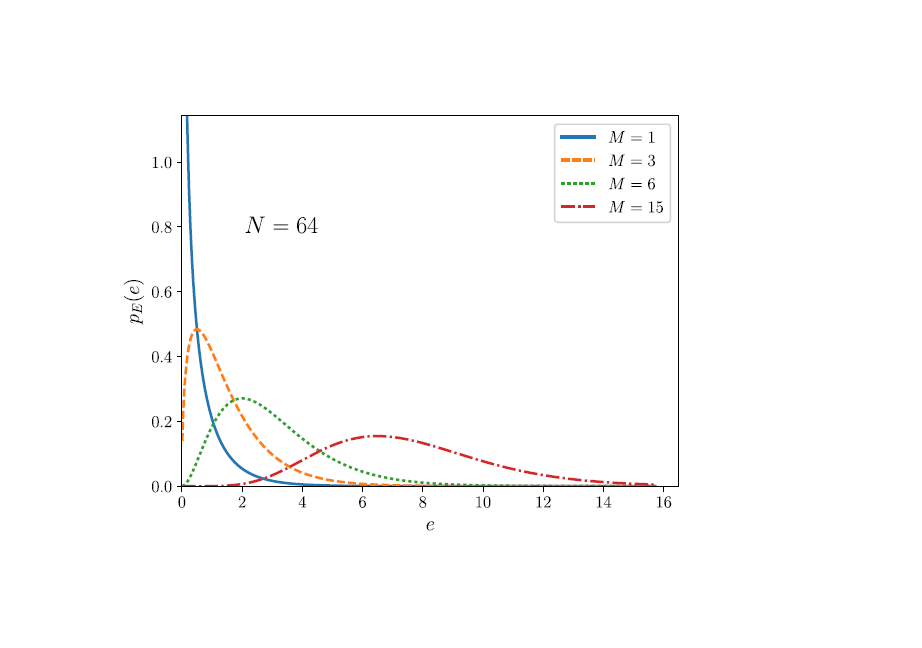ここから、ランダムに選んだ状態のエネルギーが $\varepsilon$ 以下である確率 $P_E(\varepsilon)$ は

$\displaystyle P_E(\varepsilon)=\cases{\frac{1}{\Gamma(M/2)}\gamma\left(\frac{M}{2}, \varepsilon\right) \text{ for }\varepsilon\geq0\cr 0 \text{ else }}$

となります。ここで $\Gamma$ はガンマ関数で $\gamma$ は不完全ガンマ関数と呼ばれるものです。この確率分布を用いて、エネルギーが $\varepsilon$ 以下である状態数の期待値を計算しましょう。ここでは全てのスピンを反転したような状態は、エネルギーが同じ値を取るため、同じ状態とカウントしています。ここで注意が必要なのは、planted solutionの存在から、任意の $\varepsilon$ について、必ず1つの解(すなわちplanted solution)はエネルギーが $\varepsilon$ 以下になっているという点です。この点を考慮に入れて、エネルギーが $\varepsilon$ となる状態数の期待値を計算すると

$\displaystyle \mathbb{E}(\verb|#|(E\leq\varepsilon)) =1+\left(2 ^{N-1}-1\right)P _ E(\varepsilon)= 1+(2 ^{N-1}-1)\frac{1}{\Gamma(M/2)}\gamma\left(\frac{M}{2}, \varepsilon\right)$

となります。

次に解を探すためにはどれくらいの状態を探せばよいのでしょうか。 $\mathrm{dim}\mathrm{Ker}W ^{\mathrm{T}}=N-M$ ですが、これは線形代数の問題のときでイジングスピンの時は一般にどうなるのか自明ではありません。しかし、(ここでも導出は省きますが) 実はイジングスピンの時でも $2 ^{N-M}$ 個の状態を探せばよいことが示せます。スピン反転対称性を鑑みると $2 ^{N-M-1}$ 個の状態を調べればよいことになります。

ここでランダムに $2 ^{N-M-1}$ 個の状態から選んでいき、その状態のエネルギーを調べることを考えます。何回目の試行で基底状態を選べるかを表す指標を $\tau$ とかくと、 $\tau = 2 ^{N-M-1}/\verb|#|(E = 0)$ になります。ここで丸め誤差を考慮して $\tau = 2 ^{N-M-1}/\verb|#|(E \leq \varepsilon)$ と定義しなおすと、次のような定量的に問題の難しさを測る指標を得ることが出来ます。

$\displaystyle \mathbb{E}\left(\frac{1}{\tau}\right)=\frac{\mathbb{E}\left(\verb|#|(E\leq\varepsilon)\right)}{2 ^{N-M-1}}$

基底状態を得るのに必要な試行数が $\tau$ であるため、 $\tau$ が大きくなればなるほど、つまり問題が難しくなればなるほど上の指標は小さい値となる仕組みです。この量を $Q_N(M)$ と定義して $M$ を変えた際にどの程度 $Q_N(M)$ が小さくなるかを見ていきましょう。

一番問題が難しくなる $M$ とは、言い換えると $Q_N(M)$ が最小になるような $M$ を考えていることになります。また各 $N$ について問題が一番難しくなる $M$ を調べていくと次のような線形の関係にあることが示唆されています。

$M\cong 1.63+0.073N$

(以下は論文の内容ではなく筆者の考えになります) では具体的に $Q _ N(M)$ はどれくらいの値なのでしょうか？以下のグラフがそのプロットになります。

f:id:jijinc-intern:20200714213622p:plain

ここから分かることは、一般に $Q _ N(M)$ は $N>M$ のときに非常に小さくなり得るということです。従って例えばWPEを使ってベンチマークを取ったりする際には、 $Q _ N(M)$ を最小化するような $M$ を選んでしまうと、ほとんどの場合正しい解にはたどり着きません。また、論文での議論から明らかなように $M$ を増やすほど問題は簡単になっていきますが、 $M > N$ の場合には $Q _ N(M)$ は定義は出来ますが、この量の意味を与えることが難しくなります。従って、とても実務的な観点からは、 $M > N$ の際にうまく意味づけが出来ないという点からも実は $Q _ N(M)$ の概念はそこまで便利なものではなく、 $M > N$ の時の考察が必要になってくるといえるでしょう。

実際に実装した結果

ここでは実際にWPEからイジングハミルトニアンを生成して、それをopenjijで解いた結果を載せます。

f:id:jijinc-intern:20200714230225p:plain

上の図は $N=100$ で、上から順に $M=1, 50, 99$ の場合に1000回WPEからハミルトニアンを生成し、それをアニーリングで解いた時のエネルギーヒストグラムになります。またここでplanted solutionは強磁性解としています。ここから分かるように $M$ が小さいときは低エネルギー状態が多く、 $M$ が大きいときは正しい解が出て来ています。

それでは $M=1\sim99$ で動かした際にどれほど基底状態に近いエネルギーを持つ解を出す回数が増えるかを見てみましょう。

f:id:jijinc-intern:20200714232636p:plain

$M$ が小さいときは上の議論にあるような縮退が原因で回数が増えますが、 $M$ が増大するとともに縮退が減って、その分基底状態に近いようなエネルギーを持つスピン配置にはたどり着けなくなっていきます。そして $M=80$ くらいからようやく低エネルギー状態が増え(これは基底状態そのものと考えることが出来ます。)、 $M=99$ では、おおよそ5%の割合で基底状態が求められていることになります。

上の結果はすべて強磁性解をplantした際の結果ですが、強磁性解以外だとどうなるでしょうか？次にネール状態(反強磁性解)の場合を見てみましょう。

f:id:jijinc-intern:20200714233959p:plain f:id:jijinc-intern:20200714234012p:plain

上のプロットから分かるように、反強磁性解でもおおよそ強磁性解と同じような分布になります。それでは $M=1\sim99$ で動かした際にどれほど基底状態に近いエネルギーを持つ解を出す回数が増えるかを見てみましょう。 f:id:jijinc-intern:20200720050457p:plain 基底状態が正しく求まる確率の $M$ 依存性も強磁性解とほぼ同じになります。

上の２つの例は基底状態がオーダーしている場合での結果でしたが、オーダーしていない場合はどのようになるでしょうか。基底状態 $\vec{t}$ をランダムに与えた場合は次のようになります。

f:id:jijinc-intern:20200720050205p:plain

ほぼ秩序相と同じ振る舞いですが、 $M=1$ のときはエネルギーが少し広めに分布しています。正しい解を出す確率は次のようになります。

f:id:jijinc-intern:20200720060108p:plain

従ってWPEで生成された問題は基底状態が秩序相か無秩序相かに関わらず、似たような性質を持つことが分かります。

統計力学的な議論

WPEで生成された系の振る舞いを物理サイドから考察してみましょう。

TAP自由エネルギー

WPEの親戚にあたるSKモデルなどのスピングラスで良く考察される系を解析するときには、平均場方程式を拡張したTAP方程式と呼ばれる方程式を解いて系の大まかなふるまいを理解することがあります。ここでもWPEに対応するTAP方程式及びTAP自由エネルギーを解析することでこの系のふるまいを考えたいと思います。詳しい導出はしませんが、WPEで与えられた系に対するTAP自由エネルギーは次のように表すことが出来ます。 $\displaystyle F _ {\mathrm{TAP}}(\vec{m})=-\frac{1}{2}\sum _ {i\not=j}J _ {ij} m _ i m _ j - \frac{1}{\beta}\sum _ {i=1} ^NS(m _ i) \ -\frac{1}{2}\alpha N\left((1-q)-\frac{1}{\beta}\log\left(1+\beta(1-q)\right)\right)$ ここで $\beta$ は逆温度、 $q=1/N\sum _ {i=1} ^Nm _ i ^2$ で定義されています。また $S(m _ i)$ はスピン $i$ にたいするエントロピーで

$\displaystyle S(m _ i)=-\frac{1+m _ i}{2}\log\frac{1+m _ i}{2}-\frac{1-m _ i}{2}\log\frac{1-m _ i}{2}$

で表されます。初めの2項は通常の平均場の自由エネルギーで、第3項がTAP自由エネルギー特有の項で、相互作用がWishart分布に従っていることに由来しています。自由エネルギーを最小化すると次のようなTAP方程式が得られます。

$\displaystyle m _ i = \tanh\left(\beta\left(\sum _ {i\not=j} J _ {ij} m _ j-\beta\frac{\alpha(1-q)m _ i}{1+\beta(1-q)}\right)\right)$

絶対零度 $\beta=\infty$ の場合は磁化は $\vec{m}=\vec{t}$ となりますが、有限温度でも基底状態と磁化が同じ方向になる、すなわち $\vec{m}=m\vec{t}$ と仮定して、TAP自由エネルギーを書き直します。この場合自由エネルギーは $m$ についてのスカラー関数となります。

$\displaystyle F(m) =-\frac{1}{2}m ^2\sum _ {\mu=1} ^M\sum _ {i=1} ^N \left(w _ {ii} ^\mu\right) ^2-\frac{N}{\beta}S(m)-\frac{1}{2}\alpha(1-m ^2)+\frac{\alpha N}{2\beta}\log\left(1+\beta(1-m ^2)\right)$

この表式の第一項は $O(\sqrt{N})$ でスケールするため、熱力学極限 ( $N \to \infty$ )を考える上では無視して構いません。従って次の自由エネルギー密度を考えれよいかもしれません。ばよいことが分かります。

$\displaystyle f(m)=-\frac{1}{\beta}S(m)+\frac{\alpha}{2N}\log\left(1+\beta(1-m ^2)\right)$

このエネルギー密度をプロットすると次のようになります。

f:id:jijinc-intern:20200720063046p:plain

明らかに一次転移している様子が見て取れます。

系の安定性

自由エネルギーの様子から、高温相では $m=0$ がエネルギーが最も低く、低温相では $m$ が有限の時にエネルギーが最小になることが分かりますが、それに加えて、ある温度では $m=0$ が準安定になることも見て取れます。これは１次転移の特徴の一つで、この場合は系の安定性を調べる必要があります。(細かいことをいうと準安定な相が出てくるには必ずしも１次転移である必要はありません。)そこで $m=0$ の状態が不安定になるときの温度を調べましょう。これは自由エネルギーのヘッセ行列を見ることと等価です。

$\displaystyle H _ {ij}(\vec{m})=\frac{\partial ^2F(\vec{m})}{\partial m _ i\partial m _ j}=\cases{\frac{1}{1-m _ i ^2}-\frac{2\alpha\beta m _ i ^2}{N\left(1+\beta(1-q)\right) ^2}+\frac{\alpha\beta(1-q)}{1+\beta(1-q)}\quad i=j \cr -J _ {ij}-\frac{2\alpha\beta m _ i m _ j}{N\left(1+\beta(1-q) ^2\right)}\quad i\not=j}$

従って $m=0$ の時は

$H _ {ij}=\cases{\frac{1}{\beta}+\frac{\alpha\beta}{1+\beta}\quad i=j\cr-J _ {ij}\quad i\not=j}$

ここから安定性条件は

$\frac{1+\beta(1+\alpha\beta)}{\beta(1+\beta)}>\alpha$

となります。

まとめ

本記事では真の解から解くことが難しい問題を生成する手法である Wishart Planted Ensemble と呼ばれる手法を紹介し、定量的、統計力学的な議論を行いました。生成される問題の難しさも制御できるため、アニーリング等で用いられる提案手法のベンチマークとして極めて有効だと思われます。記事中に問題を生成するためのPythonコードも用意したので、興味のある方は試してみるとよいかもしれません。