この記事の概要
Subasi et al., 2018, "Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing"を読んだので、その理解を深めるためのアウトプットとして作成したものです。
問題設定
のエルミート行列
とベクトル
があったとき、以下の連立一次方程式
を満たすを求めよ、という問題です。答えとなる
という量子状態が求まれば、この問題が解けたことになります。ここで
です。さらにには逆行列が存在し、
とします。
実際にはの精度でこの問題を解きたいので、求まった状態
が
を満たすアルゴリズムを作ることが、この論文のゴールです。
断熱量子計算
ハミルトニアン
ハミルトニアンを
のように定めます。ここで
です。さらには1量子ビットにおけるパウリ演算子、
は
の固有状態、
]はアニーリング時間を表すパラメータです。このハミルトニアンは
次元のヒルベルト空間を持ちます。これは
次元の行列
に加えて、1つの補助量子ビットを用いるためです。補助量子ビットを用いることで、
は全ての
に対して逆行列が存在することが保証されます。
基底状態とエネルギーギャップ
基底状態
は基底状態で、を満たします。これが唯一存在する基底状態です。
を
に増加させると
のように変化します。
エネルギーギャップ
上述のハミルトニアンにおける基底状態と第1励起状態のエネルギーギャップは
を満たします。ここでは行列
の条件数です。
条件数とは、その問題のコンピュータでの数値解析しやすさの尺度でその問題がどれだけ数値解析に適しているかを表す指標です。小さな値ほど解析しやすい良条件で、大きな値ほど解析しにくい悪条件となります。
Randomization Method (RM)
通常の量子アニーリングではを連続に変化させます。しかしここでは離散的に変化させることで、基底状態の近似射影測定を効果的に計算することができます。このとき、離散的にした
を一定に保つ時間間隔をランダムに決定するため、これをRandomization Method (RM)と呼びます。
RMの計算時間はであることが知られています。ここで
はパスの長さ
そしてはハミルトニアンの最小エネルギーギャップです。
アニーリングスケジュール
HHLの断熱量子計算アルゴリズムにおいては
というアニーリングスケジュールを組むことで、基底状態を求めることができます。ここで
です。このアニーリングスケジュールをのように
個に分割します。ここで
、そして
です。 このRMステップ数は
で与えられます。このように
を選ぶことで
となります。
アルゴリズムと計算時間
において、ランダムな時間の長さ
の元で状態を時間発展させます。
]の一様乱数です。ここで時間発展させるとは、以下のように演算子を次々に掛け合わせていくことに対応します。
この方法で解を求めるのにかかる総計算時間は、を計算して
と算出されます。
アルゴリズムの改良 (エネルギーギャップの増幅)
シンプルな考え方として、このアルゴリズムを高速化する方法の1つにのエネルギーギャップを大きくすることが考えられます。そのためには、行列の固有値
を大きくするような、例えば固有値を
となるような変換を施せば良いです。
そこで新しいハミルトニアンとして、以下のようなものを考えます。
ここでは1つの補助量子ビットにかかる上昇・下降演算子です。このハミルトニアンは
次元のヒルベルト空間を持ちます。さらに
となります。上の行列は各ブロックがの行列となります。
を用いると、対角ブロックはそれぞれ
と書けます。このことから、このハミルトニアンは元々のハミルトニアン
と同じエネルギースペクトルを持ちます。
この変換によって、エネルギーギャップはとなります。よって、時間間隔も
]の一様乱数として選ぶことができます。このとき同様に
を計算して
となり、に対して線形時間で計算を終了させることができます。
# 数値実験
数値実験結果を以下に示します。この図のの添字のデータは
を用いた計算、
の添字のデータは
を用いた計算結果です。
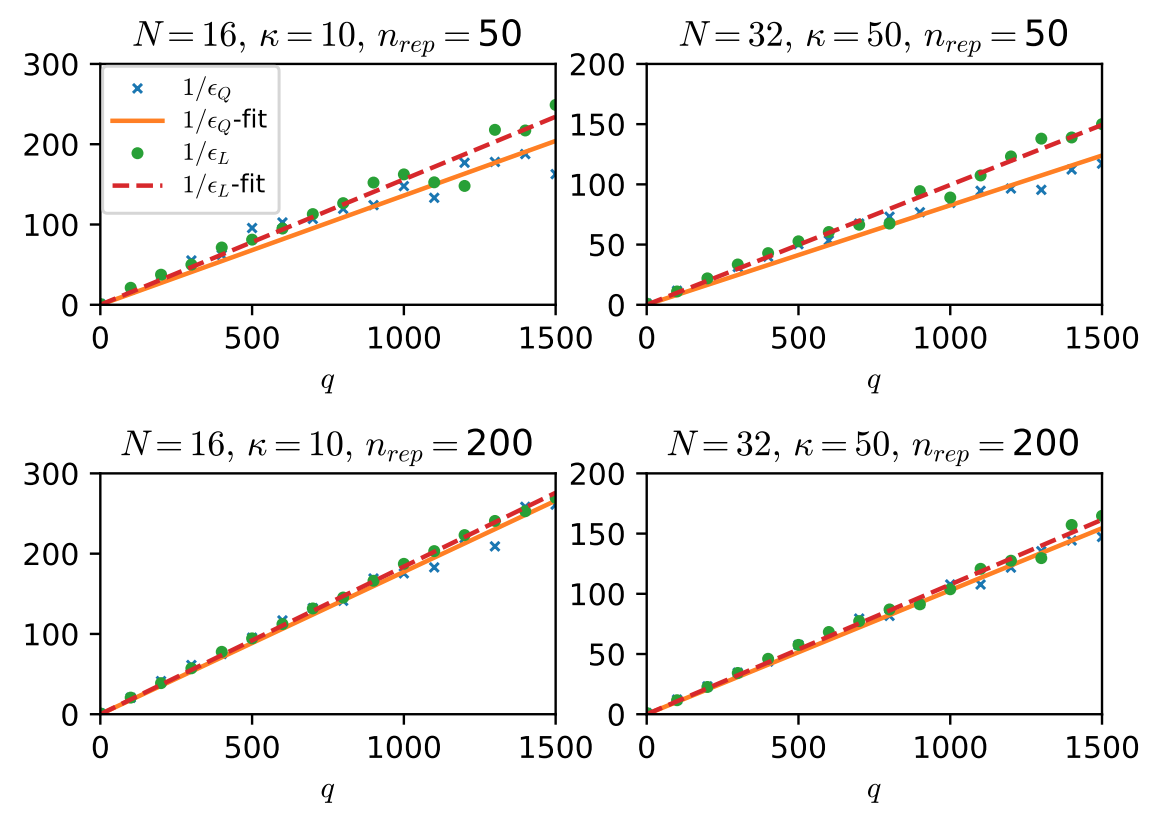
横軸はRM step数、縦軸はエラーの逆数です。各パネルの
は行列
の次元
、
は行列
の条件数、
はアルゴリズムの繰り返し回数です。
に対してほぼ線形になっていることがわかります。
結言
線形時間で連立一次方程式を解く、その手法として断熱量子計算とRMを組み合わせる方法及びそれを理解するための理論をご紹介しました。
参考文献
文責
中村翔、株式会社Jij
Sho K. NAKAMURA, Jij inc.
憂いの篩 -Pensieve-
※ 疑問点や間違いなどございましたら、お気軽にブログ上でご質問ください。