Jij Tech Blog

Jij inc.の開発日記です

量子コンピュータでLHC高エネルギー実験データ探索

量子ゲート 物理

この記事の概要

Armenakas & Baker, 2020, "Application of a Quantum Search Algorithm to High-Energy Physics Data at the Large Hadron Collider"を読んだので、その理解を深めるためのアウトプットとして作成したものです。

序章: Groverの量子探索アルゴリズム

概要

グローバーのアルゴリズムは整列されていないデータベースから、特定のデータを探索するための量子アルゴリズムです。ソートされていない$N$個のデータに対して$\mathcal{O}(\sqrt{N})$回のクエリ(オラクルを呼ぶ操作のこと)で解を見出すことができます。古典コンピュータでは$\mathcal{O}(N)$回のクエリが必要になります。このため、このアルゴリズムを用いることで二次(Quadratic)加速が実現されます。

オラクルやクエリに関しては以下の記事をご覧ください。

jijtech.hatenablog.com

jijtech.hatenablog.com

オラクルさえ構成することができれば、グローバーのアルゴリズムはあらゆる古典アルゴリズムの全探索部分を高速化することができます。今回はこれをLHCの大規模データに応用したものです。

アルゴリズム

$N$個の要素からなデータベースから$M$個の解を探索することを考えましょう。要素のラベルを$n$桁のビット列$x = x_1 x_2 \cdots x_n$とします。

  1. 全ての状態の重ね合わせ状態$|s \rangle = \frac{1}{\sqrt{N}} \sum_x | x \rangle$を用意します。
  2. オラクル$U_w$(解に対する反転操作)を作用させます。
  3. 初期状態$|s \rangle$を対称軸にした反転操作$U_s$を作用させます。
  4. Step 2, 3を$k$回繰り返します。
  5. 測定します。
Step 1

初期状態$|0 \cdots 0 \rangle$に対して全ての量子ビットにアダマールゲート$H$を作用させます。

\displaystyle{ (H\otimes \cdots \otimes H) | 0\cdots 0 \rangle = \frac{1}{2^{n/2}}(|0\rangle + |1\rangle) \otimes \cdots \otimes (|0\rangle + |1\rangle) := | s\rangle }

Step 2

オラクルを作用させます。ここではオラクルとして、「入力$|x\rangle$に対して$x$が解なら-1をかけて位相を反転し、解でなければ何もしない」という演算を考えることにします。ここでは補助ビットは省略して$U_w$を記述すると以下のようになります。

\displaystyle{ U_w = I -2\sum_{w\in 解} |w\rangle \langle w| \\ U_w |x\rangle = \left\{ \begin{array}{c}|x\rangle & (x \ {\rm is \ not \ solution}) \\ -|x\rangle & (x \ {\rm is \ solution}) \end{array} \right. }

入力が解であるときにだけ位相反転を行うので、オラクル$U_w$は「解に対する反転操作」と呼ばれます。

Step 3

全ての状態の重ね合わせ$|s\rangle$を対称軸とした反転操作$U_s$を作用させます。

\displaystyle{ U_s = 2 |s \rangle \langle s| -I }

$|s\rangle$に直行する状態を$|s_\perp \rangle$とすると、この演算子は入力状態$|\psi \rangle = a | s\rangle + b|s_\perp \rangle$に対して

\displaystyle{ U_s | \psi \rangle = a |s\rangle - b|s_\perp \rangle }

のように作用します。ご覧のように$|s_\perp\rangle$に比例する部分の位相だけを反転させます。

Step 4

Step 2, 3で示した2つの反転操作 U_w, U_sを繰り返し作用させます。およそ$\mathcal{O}(\sqrt{N/M})$回の繰り返しを行った後で測定することにより、十分高い確率で解を得ることができます。すなわちオラクルを呼ぶ回数は$\mathcal{O}(\sqrt{N})$で十分であることがわかります。

Step 5

ここまでのステップで状態は (U_s U_w)^k |s\rangleとなっています。$k$はStep 2, 3の繰り返し回数です。この状態は解 wに対応する状態 |w\rangleの係数の絶対値のみが非常に大きくなっています。よってこの状態を計算基底で測定すれば高い確率で解 wのビット列が得られます。

幾何学的な説明とアルゴリズムまとめ

次のように2つの状態$|\alpha \rangle, | \beta \rangle$で張られる2次元平面を考えます。

\displaystyle{ |\alpha \rangle = \frac{1}{\sqrt{N-M}}\sum_{x\in 解ではない} | x\rangle \\ |\beta \rangle = \frac{1}{\sqrt{M}}\sum_{x\in 解} | x\rangle }

初期状態である、全ての状態の重ね合わせ状態|s\rangleは次にように表されます。

\displaystyle{ |s \rangle = \frac{1}{\sqrt{N}} (\sum_{x\in 解ではない} |x \rangle + \sum_{x \in 解} |x\rangle) = \sqrt{\frac{N-M}{N}} | \alpha \rangle + \sqrt{\frac{M}{N}} |\beta \rangle }

よって、|s\rangleはこの2次元平面内のベクトルであることがわかります。特に$\cos\frac{\theta}{2} = \sqrt{\frac{N-M}{N}}, \sin\frac{\theta}{2} = \sqrt{\frac{M}{N}}$を満たす角度$\theta$を用いれば

\displaystyle{ |s \rangle = \cos \frac{\theta}{2} |\alpha \rangle + \sin \frac{\theta}{2} | \beta\rangle }

と書けます。これを図示すると以下の左図ようになります。

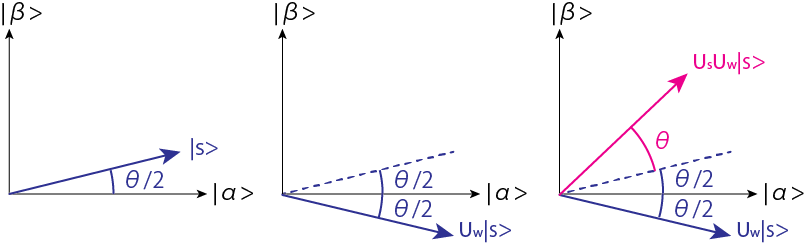
A figure of geometrical explanation for Grover's algorithm
グローバーアルゴリズムの幾何学図による説明。

この平面内ではオラクル U_wは$|\beta\rangle$に対する反転操作( U_w |\alpha \rangle = | \alpha \rangle, U_w | \beta \rangle = -|\beta \rangle)です。よって U_wを作用させた後(真ん中図)、$|s\rangle$を対称軸とした反転$U_s$を作用させると$|\alpha \rangle, |\beta \rangle$ 平面内で角度$\theta$の回転が行われたことになります(右図)。

グローバーのアルゴリズムではこの操作を繰り返し行うので、$k$回繰り返したあとの状態は

\displaystyle{ (U_s U_w)^k |s\rangle = \cos \frac{(2k+1) \theta}{2} |\alpha \rangle + \sin \frac{(2k+1) \theta}{2} |\beta \rangle }

のようになっています。実際の探索を考えたとき、$N \gg M$となっているので$\theta$の値は0に近い正の数になっています。よって$|s\rangle$に U_s U_wを作用させるたびに$|\alpha\rangle$の係数が減少し、$|\beta \rangle$の係数が増加します。$|\beta\rangle$は全ての解の状態の重ね合わせでできていました。このことからこの操作を繰り返したのちに測定を行うと、解が出力される確率が高くなることを示しています。

以上のStepで状態がどのように変化するかを以下の図に示します。

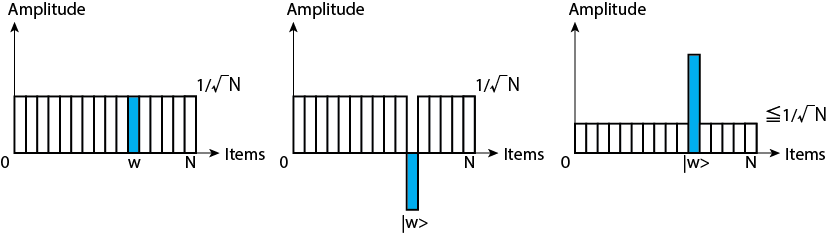
A figure of state transition with Grover's algorithm
グローバーアルゴリズムによる状態の変化。

Step 1で初期状態$|s\rangle$を作成します(左図)。Step 2で$U_w$を作用させることで、解である状態 |w\rangleの位相を反転させます(真ん中図)。Step 3で$U_s$を作用させることで、解である状態は位相を反転させつつ振幅を増幅させます。その他の状態は振幅を減衰させます。Step 2, 3を繰り返すことで、解である状態のみを選び出すくとが可能となります。

最適な繰り返し回数の見積もり

U_s U_wを作用させる回数$k$、すなわちオラクルを呼ぶ回数がどの程度になるかを評価します。 (U_sU_w)^k |s\rangleが$| \beta \rangle$に最も近くなるのは$(2k+1)\theta/2 \sim \pi/2$となるときです。すなわち$k$の値が

\displaystyle{ R = {\rm ClosestInteger}(\frac{\pi}{2\theta}-\frac{1}{2}) }

となるときです。ここでClosestInteger(...)は...に最も近い整数を表します。この値の上限の評価を行います。$\theta$について成り立つ式

\displaystyle{ \frac{\theta}{2} \geq \sin \frac{\theta}{2} = \sqrt{\frac{M}{N}} }

を使います。

\displaystyle{ R \leq (\frac{\pi}{2\theta} - \frac{1}{2} ) +1 = \frac{\pi}{2\theta} + \frac{1}{2} \leq \frac{\pi}{4} \sqrt{\frac{N}{M}} + \frac{1}{2} }

よって$R$は$\mathcal{O}(\sqrt{N/M})$程度となり、グローバーのアルゴリズムが$\mathcal{O}(\sqrt{N})$の計算量で動作することがわかります。

序章: LHC (Large Hadron Collider)とヒッグス粒子

LHC概要

LHC加速器はヨーロッパ共同原子核研究機構(CERN)により建設され、2009年から運転を開始した世界最大のハドロン衝突型加速器です。LHCは円形構造をしており、その周長は27kmになります。フランスとスイスの国境をまたぎ、およそ地下100mの位置に実験施設があります。

陽子同士を13TeVという超相対論的速度で衝突させることで素粒子反応を見ることを目的とした実験施設です。

LHCはヒッグス機構が予言するヒッグス粒子(Higgs boson)の発見から、2013年のノーベル物理学賞受賞に大きく貢献したことで有名です。

ヒッグス粒子の崩壊

ヒッグス粒子の崩壊過程の1つに、以下のようなものが考えられています。

\displaystyle{ H \rightarrow ZZ^\ast \rightarrow 4l }

$H$はヒッグス粒子、$Z$はZボソン、$Z^\ast$はoff-shell Zボソン、そして$l$はレプトンです。最終的に1つのヒッグス粒子が4つのレプトンに崩壊する反応を表しています。しかし、珍しい崩壊の仕方として、以下のような反応もあると考えられています。

\displaystyle{ H \rightarrow ZZ_d \rightarrow 4l }

ここで$Z_d$はダークセクターのZボソンで、素粒子の標準理論(Standard Model)の領域を超えた粒子です。

この論文の独創性

LHCの中でもATLASという観測装置のデータを量子コンピュータの量子ビットにエンコードします。そのデータベースにグローバーのアルゴリズムを適用することで、見つけたい素粒子反応を発見することができることを示しました。ただしそのままエンコードを行い、さらにグローバーのアルゴリズムを適用すると、量子ゲートの数が多くなります。するとNISQデバイス上では量子でコヒーレンスによるエラーのために、返って精度が悪くなります。そこでデータエンコードに工夫をすることで、このエラーを回避する方法を考案しました。

LHCのデータベース構造

衝突させているビームに垂直な方向のレプトンの運動量がデータベースには記録されています。レプトンはそれ自身のエベント数も記録されています。また同じイベントないのレプトンを区別するために、インスタンス値が割り当てられています。あるイベントで最初に検出されたレプトンはインスタンス値0を持ちます。あるイベントで2番目に検出されたレプトンはインスタンス値1, 3番目に検出されたレプトンはインスタンス値2を持つ、のように番号割り振りを行います。

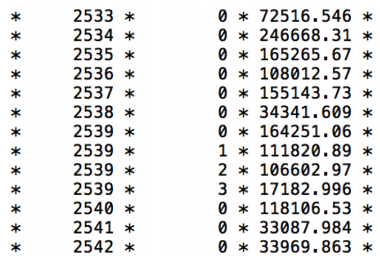
A sample of LHC experimental data
LHCデータのサンプル。

上の数値データは実際のLHCデータベースです。3列の数字のうち、真ん中の整数がインスタンス値を表しています。0~3の値があるということは、1つのイベントで4つのレプトンが検出されたことを示しています。

データのエンコーディング

量子探索アルゴリズムでデータを探索するには、量子コンピュータ上の量子ビットに(古典)データを対応させる必要があります。

そのまま実装する場合の考え方

以下では4つのレプトン検出を、例として5つの量子ビット系に配置する場合をご紹介します。以下では5つの量子ビットをそれぞれq[0], q[1], q[2], q[3], q[4]と名付けます。
q[0]とq[1]は検出器が検出したレプトンの通し番号を表す量子ビットです。
ATLASで検出された各レプトンはインスタンス値が付与されています。そして私たちが検索したい状態に対応するのはインスタンス値=3の状態です。インスタンス値をq[2], q[3]で表現します。
q[4]は補助量子ビットとして用います。

工夫した実装の考え方

今度はq[0]とq[1]で0~3のインスタンス値を表現します。そしてq[2], q[3], q[4]で0~7の値を表現することを考えます。もしインスタンス値が3の場合は量子状態は$|\_\_\_11\rangle$のように書かれます。これはq[4], q[3], q[2]は任意の値、そしてq[1], q[0]は両方ともに$|1\rangle$状態になっていることを表しています。全ての量子ビットを$|0\rangle$で初期化しておきます。
通し番号が0のときはXゲートを作用させません。$|000\_\_\rangle$のままです。
通し番号が1のときは1つのXゲートをq[2]にのみ作用させ、$|001\_\_\rangle$のようにします。
通し番号が2のときは1つのXゲートをq[3]にのみ作用させ、$|010\_\_\rangle$のようにします。
通し番号が3のときは1つのXゲートをq[4]にのみ作用させ、$|100\_\_\rangle$のようにします。
このようにして初期状態にデータを流し込むことで量子ゲートの数を減らすことに成功し、エラーを軽減することに成功しました(後述)。

そのまま実装した場合の実行結果

シミュレータでの実行

次の図は3つの量子ビットを用いて量子探索を行った場合の結果です。ここでは$|111\rangle$の状態が求めたい状態であるとします。

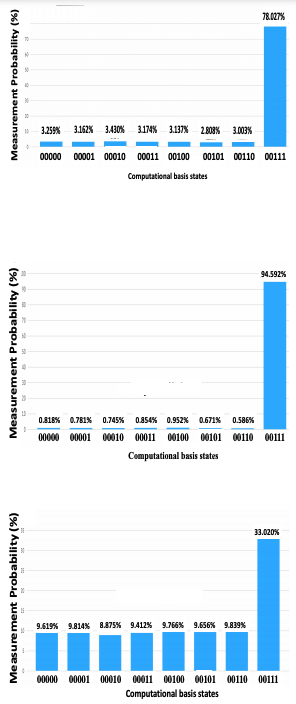
Probability of target state measurement with multiple iterations
グローバーアルゴリズムの繰り返し回数による測定確率の変化。

一番上の図はグローバーの繰り返し回数を$k=1$としたとき、真ん中の図は$k=2$、そして一番下の図は$k=3$としたときの測定確率です。$k=1$のとき$|111\rangle$を見出す確率は78%、$k=2$のときは95%、$k=3$のときは33%という結果を得ています。

先ほどのグローバーのアルゴリズムの繰り返し回数の見積もり

$$R \simeq \frac{\pi}{4} \sqrt{\frac{N}{M}}$$

において、検索する状態の総数を$N=2^3$、そして見つけたい状態の数を$M=1$とすると、$R\simeq \pi \sqrt{2^3} /4 \sim 2.22$となります。最適な繰り返し回数が$k=2$であることが数値実験からもわかります。

量子コンピュータ実機での実行

次の図はQiskitシミュレータでの実行結果です。

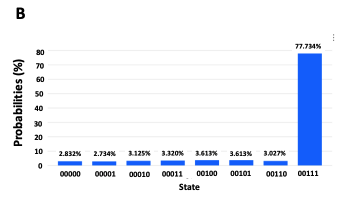
Grover's algorithm applied to three-qubit system on Qiskit simulator
3量子ビットでグローバーアルゴリズムを実行、Qiskitシミュレータの場合。

さらに次の図はIBMの量子コンピュータ実機での実行結果図です。

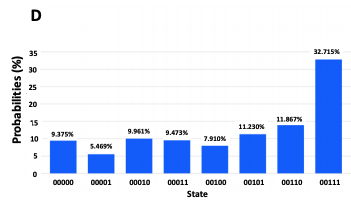
Grover's algorithm applied to three-qubit system on IBM quantum computer.
3量子ビットでグローバーアルゴリズムを実行、IBMの量子コンピュータ上での実行。

シミュレータでは77%の確率で見つけたい状態を見つけることができますが、量子コンピュータ実機では33%になっています。これはNISQデバイスの量子でコヒーレンスによるエラーのためです。

工夫した実装の場合の実行結果

以下の図は5量子ビットで、量子コンピュータ実機上で量子検索アルゴリズムを実行したときの結果です。

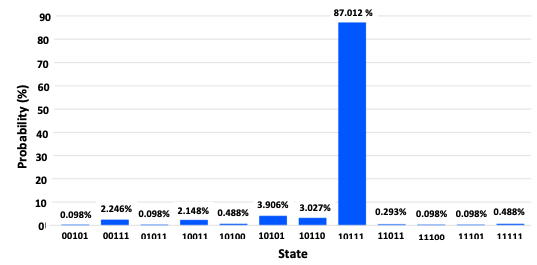
A histogram of final result with improved encoding circuit
工夫したエンコーディングでの実行結果。

8192回の試行のうち7128回(およそ87%の確率)で求めたい状態を得ることができました。

結言

今回はグローバーのアルゴリズムの応用例の1つとして、LHC高エネルギー実験データから素粒子崩壊を探索する例をご紹介しました。

参考文献

文責

中村翔、株式会社 Jij
Sho K. NAKAMURA, Jij Inc.
憂いの篩 -Pensieve-

※ 疑問点や間違いなどございましたら、お気軽にブログ上でご質問ください。