この記事は2021年物理学アドベントカレンダーの3日目です。
2021年のアドベントカレンダーということなので2021年のノーベル物理学賞の一つのスピングラスを題材にしたいと思います。
さっそく本題のOpenJijを使った数値計算について知りたい方はここに飛んでください。
パリージさんはスピングラスという模型の解析手法についての功績が評価されての受賞となりました。スピングラスは物理の統計力学における複雑な磁性体の数理モデルを表す系ですが、その後この解析手法は今の深層学習の元となるニューラルネットの解析など様々な複雑系の解析への応用がなされており物理を飛び出して非常に多くの分野に影響を与えています。
日本物理学会のノーベル賞解説に大関先生が解説を書かれているのでぜひ読んでみてください(https://www.jps.or.jp/public/2021nobel1.php)。
この記事ではそのスピングラスの簡単な解説と手軽に使えるOpenJijというイジングモデルの数値計算ツールを使って実際にスピングラスの数値計算をしてノーベル賞の公式ページにあるPDF(https://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf)にある図を再現することを目標にします。
読者には学部の統計力学でイジングモデルについて一応学んだことがあるくらいを想定します。
イジングモデルと相転移
簡単にイジングモデルについて紹介しておきます。
イジングモデルは磁石を表すモデルで小さな磁石(スピン)の集まりを考えてシンプルな相互作用のみを考えます。
$$E = -\sum_{i, j}J_{i, j}\sigma_i \sigma_j,~\sigma_i \in {-1, 1}$$
イジングモデルのエネルギーを見るとわかるように相互作用係数$J_{ij}$が正の場合は各スピン同士が同符号の場合がエネルギーが下がります。この$J_{ij}$は結合しているスピンの揃いやすさを表しています。すべての$J_{ij}$が正の場合、ボルツマン分布
$$p(\{\sigma_i\}_{i=1}^{N}) = \exp\left(-\beta E(\{\sigma_i\}_{i=1}^{N})\right)/Z$$
に従ってスピン配列$\{\sigma_i\}$を生成して、その各サンプルを使って以下の磁化
$$m = \frac{1}{N}\left\langle \sum_i\sigma_i\right\rangle$$
を温度$T$を横軸にプロットするとある温度より低いところで急激に$m$が有限の値を持つようになります。これが磁性体の相転移を表しています。$m$は各スピンの揃い具合を表していて、温度が低いところでは多くのスピンが同じ向きを向くことで大きな磁化を作ります。
スピングラス
では$J_{i, j}$がもっと複雑な値を持っていたらどうでしょうか。特に$i, j$によって全く異なる値を持っている時にうまく統計力学的な解析によって相転移のようなマクロな物理現象を見出すことはできるでしょうか。
簡単な強磁性イジングモデル($J_{ij}$がすべて正)の場合は系全体を特徴づける量として磁化が導入されましたが、$J_{i, j}$がバラバラな値を持っていると、エネルギーの低いスピン配列も同様にバラバラになっていると考えられます。そのため磁化のように単純にスピンの値を足し算してしまうと磁化は0になってしまうため温度が高い時と温度が低い時で区別がつきません。
このため$J_{i, j}$がランダムな分布の場合は磁化ではなく、別の特徴づけが必要となります。その特徴を見出す解析手法がレプリカ法です。
レプリカ法
系の自由エネルギーを解析すれば、各温度での系の安定な状態を見つけることができます。自由エネルギーは分配関数の対数を取れば計算できるのでした。なので分配関数の対数を計算することを考えます。これはランダムな相互作用の時でも同じです。
しかし対数を取ってもこれ以上計算できないので対数と極限に関する以下の恒等式を用います。
$$\ln Z = \lim_{n\rightarrow 0}\frac{Z^n-1}{n}$$
こうするうことで分配関数の対数ではなく$Z^n$を計算すれば良いことになりました。$Z^n$は$\ln Z$に比べると計算が楽になるのでこのまま$Z^n$を計算していきます。
$n$は極限を取っているので実数なのですが、一旦整数だと思うことにします。そうすると$Z^n$は
$$Z^n = \left(\sum_{\sigma^{(1)}} \exp \left[-\beta H(\sigma^{(1)})\right]\right) \left(\sum_{\sigma^{(2)}} \exp\left[-\beta H(\sigma^{(2)})\right]\right) \cdots $$
という風にかけて独立な同じ系を$n$個用意した系の分配関数とみなすことができます。このように$Z^n$の$n$をいったん整数だとみなして$Z^n$を計算してその結果の$n$を$n \rightarrow 0$へと外挿します。これをレプリカ法と呼びます。
急に$n$を整数だと思ってその後外挿するなんて乱暴だと思われるかもしれませんが、これが実際これまで多くの有用な結果を導きだしてきています。こちらの数学的な正当性についてや条件などについては詳しくないので別の文献を参照していただければと思います。
このあとレプリカ法では上記の手続きにおいて$n$を整数だと思って$n$個のレプリカに対する分配関数を計算していくのですが、この記事では理論的な計算ではなく数値的にレプリカを用意してスピングラスの秩序を見ていきたいと思います。
Sherrington-Kirkpatrick 模型
スピングラスの計算をするときに理論的にも扱いやすいSherrington-Kirkpatrick 模型(SK模型)を題材にします。SK模型は全結合のランダム相互作用のある系で以下のハミルトニアンで記述されます。
$$H =- \sum_{i < j}J_{ij}\sigma_i\sigma_j - h\sum_i\sigma_i$$
ここで相互作用係数$J_{ij}$は平均が$J_0/N$で分散が$J^2/N$のガウス分布から生成されているとします。
$$J_{ij} \sim \mathcal N(J_0/N, J^2/N)$$
この系のマクロな特徴づけを以下の各レプリカ$\alpha, \beta$の間の内積で行うことにします。
$$\sum_i \langle\sigma_i^\alpha\rangle \langle\sigma_i^\beta\rangle$$
$\sigma_i^\alpha \sigma_j^\beta$はそれぞれレプリカ$\alpha$の$i$番目のスピンとレプリカ$\beta$の$j$番目のスピンを表しています。$\langle \cdot \rangle$はボルツマン分布による平均値です。さらにガウス分布から生成している$J_{ij}$についての平均を$[\cdot ]$で記述することにすることにして以下の$q_{\alpha, \beta}$を定義します。
$$q_{\alpha, \beta} = \left[\sum_i \langle\sigma_i^\alpha\rangle \langle\sigma_i^\beta\rangle\right]$$
この$q_{\alpha, \beta}$がスピングラスを特徴づけるスピングラス秩序変数となります。磁化 $m = \sum_i \langle\sigma_i\rangle$が有限の値を持つときスピングラス変数も0ではない量になりますが、逆にスピングラスのようにスピン配列はバラバラでも配列が時間的に固まってしまっている場合は磁化$m$は0になりますが、スピングラス秩序変数は有限の値を持ちます。
この$q_{\alpha, \beta}$はレプリカ法による分配関数の計算の際に積分変数として表れてきて、スピングラスの理論的な解析のキーとなる変数なのですが、$q_{\alpha,\beta}$は人工的に導入したレプリカの番号$\alpha, \beta$に依存していますが、人工的に導入したパラメータなので、依存しなくてもよい気がします。なのでまず理論的に解析する一歩としてはこの$\alpha, \beta$の依存性について無視できること(レプリカ対称性 $q_{\alpha, \beta} = q$)を仮定して計算を進めます。このようにして$\beta, J_0$というマクロなパラメータだけで$m, q$といった秩序変数の解を求めることができます。このような解をレプリカ対称解と呼びますが、レプリカ対称性を仮定したことで、エントロピーが負になるようなパラメータ領域があり、物理的に正しくない結果を導いてしまいます。今回パリージさんがノーベル賞を受賞したのはこの$q_{\alpha, \beta}$に関して、解析的に計算を進めることができつつ、レプリカ対称解の問題を解決する$\alpha, \beta$の依存性、つまりレプリカ対称性の破り方を発明した功績が評価されています。
OpenJijを使ったモンテカルロ計算
ではさっそくスピングラス秩序変数をOpenJijで計算していきましょう。
OpenJijはイジングモデルを使ったモンテカルロシミュレーションを気軽に行うことができるOSSライブラリです。
pip install openjij
で気軽にインストールすることができます。
OpenJijではシミュレーテッドアニーリングを実行する関数がついていますが、その温度スケジュールを任意に操作することができます。そのため温度を一定に設定することで一定温度からのモンテカルロサンプリングを行うことが可能です。その機能を使ってイジングモデルのモンテカルロサンプリングを行ってスピングラス秩序変数の計算に必要な平均値を計算して、各温度で$q$の分布がどうなるかを確認してみましょう。
SK模型の用意
まずSK模型のイジングモデルを生成する関数を用意します。OpenJijではイジングモデルの相互作用係数を$i, j$をキーとして相互作用の大きさを値とした辞書型で受け付けるのでその形でSK模型を生成します。
import numpy as np def sk_model(N: int) -> Dict[Tuple[int, int], float]: J = {} for i in range(N): for j in range(i+1, N-1): J[i, j] = -1*np.random.normal(0, 10/N) return J
ここでは縦磁場無しで、平均値0, 分散が$1/N$のガウス分布から相互作用係数を生成します。
OpenJijを使った一定温度でのモンテカルロシミュレーション
ではさっそくOpenJijを使ってイジングモデルのモンテカルロシミュレーションを行います。
OpenJijでは温度スケジュールを 逆温度とその温度でのモンテカルロステップ数の組み合わせの配列で指定します。具体的な実装を見ていきましょう。
import openjij as oj # beta=5で100モンテカルロステップ実行 beta = 5 mcs = 100 beta_schedule = [[beta, mcs]] # [[beta, mcs], [beta2, mcs2]]とすると途中で温度が切り替わる # OpenJijのシミュレーテッドアニーリングはこのスケジュール機能で温度を下げていくスケジュールを生成してアニーリングを行っている num_reads = 10 sampler = oj.SASampler() # num_reads を指定することで独立にnum_reads個のスピン配列をサンプルしてくる response = sampler.sample_ising(h={}, J=sk_model(N=10), schedule=beta_schedule, num_reads=num_reads) print(response.record["sample"])
これで完了です。帰ってきた10個のスピン配列がプリントされます。SKモデルから生成してサンプリングした結果なのでバラバラな結果が出力されると思います。
ここで注意しないといけないのがOpenJijの引数で指定するJとhは以下のハミルトニアンにおけるJ, hです。
$$H = \sum_{i, j}J_{ij}\sigma_i\sigma_j + \sum_i h_i \sigma_i$$
物理の教科書などの定義とはJ, h の符号が逆であることに注意してください。
まずここまで出来たら sk_model の平均値を少し変更したり、betaを変更してみたりして結果が変わることを確かめてみてください。
スピングラス秩序変数の計算
ではさっそくSK模型のスピングラス秩序変数を計算しましょう。
from typing import Dict, Tuple import numpy as np import openjij as oj import matplotlib.pyplot as plt from openjij.sampler import response def sk_model(N: int) -> Dict[Tuple[int, int], float]: J = {} for i in range(N): for j in range(i+1, N-1): J[i, j] = -1*np.random.normal(0, 10/N) return J num_system = 100 # Jの平均のためのサンプリング回数 N = 50 # スピンの数 num_replica = 50 # レプリカの数 mcs = 500 # モンテカルロステップ数 beta_list = 1/np.array([0.1, 0.5, 1, 2, 5]) # 掃引する逆温度 q_list = [] for beta in beta_list: q_beta = [] qab_beta = [] for _ in range(num_system): # Jに関する平均のためのループ # スピングラスは最初から低温にしてしまうと全然動かないことがあるので少しアニールする beta_schedule = [[beta/10, 100], [beta/2, 100], [beta, mcs]] # SK模型の相互作用係数 Jsk = sk_model(N = N) # OpenJijを使ったサンプリング sampler = oj.SASampler() response = sampler.sample_ising(h={}, J=Jsk, schedule=beta_schedule, num_reads=num_replica) # num_reaplica個のレプリカの結果を取得 samples.shape == (num_replica, N) samples: np.ndarray = response.record["sample"] # レプリカ間の全組み合わせの内積を計算 q = 1/N*np.einsum("ai, bi -> ab", samples, samples) q_beta.append(q) q_list.append(np.array(q_beta).flatten()) beta_index = 0 plt.title("T = {}".format(1/beta_list[beta_index])) plt.hist(q_list[beta_index], bins=20) plt.show()
beta_index を変えることで各温度でのスピングラス秩序変数$q$の分布をみることができます。
例えば温度が低いところだと
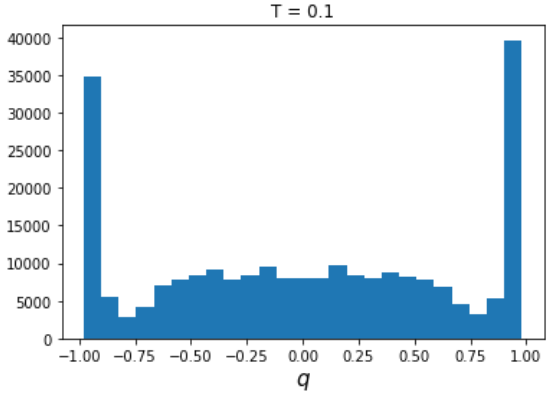
少しずつ温度を上げていくと

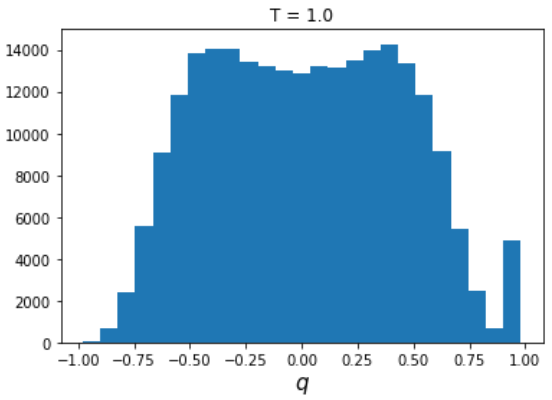
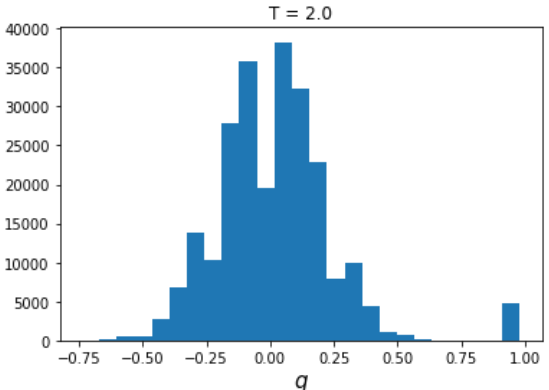
このように分布が q=0に近くなっていきます。これは温度揺らぎによってスピンがバラバラに動き、レプリカ間のオーバーラップがほぼなくなっていく様子を表しています。
今回は古典スピン系のスピングラスの数値計算をOpenJijで行う方法を紹介しました。OpenJijでは横磁場を入れた量子イジングモデルの量子モンテカルロシミュレーションも行うことが可能なので今度は量子系のシミュレーション方法についても解説したいと思います。
参考文献
スピングラスに関する理論を知りたい方は以下の書籍がおすすめです。
- 西森 - スピングラス理論と情報統計力学