量子アニーリングを用いた幾何学圧縮の最適化

この記事の概要

2020年3月に投稿されたFeld et al., "Optimizing Geometry Compression using Quantum Annealing"を読んだので、その理解を深めるためにアウトプットしたものです。

この記事の概要
論文概要
背景
- CSG木と抽出問題
関連研究
CSG木の抽出問題
結言
参考文献
文責

論文概要

幾何学データを圧縮する方法の改良は3次元コンピュータビジョンのアプリケーションにとって重要なものです。本論文では量子アニーリングを用いて、CSG(Constructive Solid Geometry, 空間領域構成法)に基づいた3次元ポイントクラウドの圧縮パイプラインを提案しました。パイプラインのキーとなるのは、解く問題をNP完全問題にマッピングして量子アニーリングで解くという部分です。ここでは最大クリーク探索問題と最小被覆問題の応用としての幾何学圧縮をご説明いたします。

背景

CSG木と抽出問題

3Dモデルの表面Sは、基本的な形Pの集合を組み合わせてできる木 $\Phi (P)$ で構成することができます。その木は、葉としてにブーリアン演算( $\cup$ : 和集合、 $\cap$ : 共通部分、 $\bar{}$ : 差集合)と基本構成要素Pを持ちます。これをCSG木と呼びます。例として以下の図のようなものがあります。

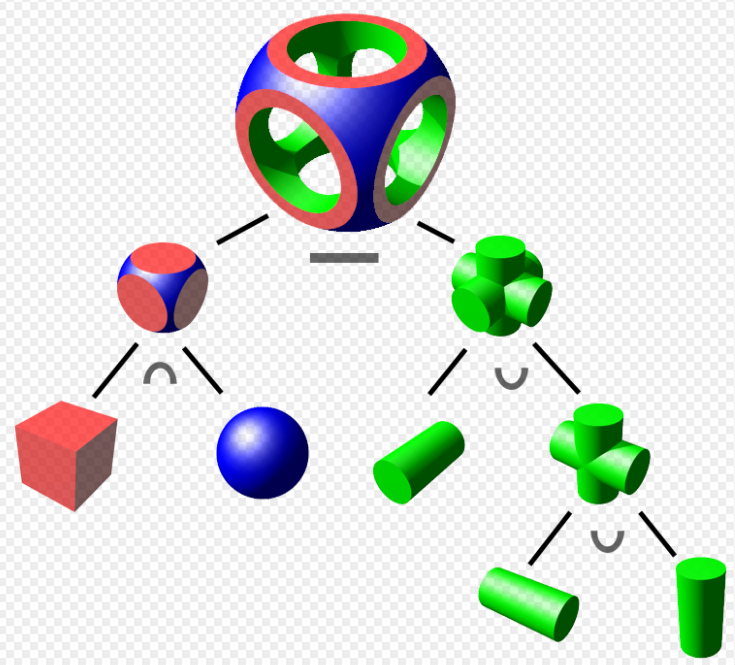
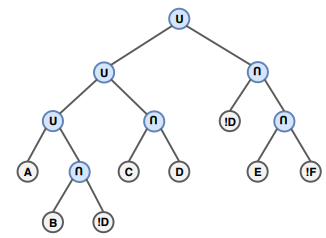
Optimal CSG tree for surface S — 物体表面Sを作る最適化されたCSG木

$S = \Phi (P)$ は物体表面を一意に決定しますが、その表面を構成するための木は無数に存在することがあります。よって同じ表面を表現するにしても、その木のサイズ(例えば葉の枚数など)によって必要なデータサイズが変わります。表面Sを構成するための木の最小サイズを求める問題は、計算量理論ではNPに分類され、ブーリアン関数の簡単化問題(Boolean funciton simplification)に等価となります。

ポイントクラウドからCSG木を作成するための一般的なパイプライン構成を次の図に示します。

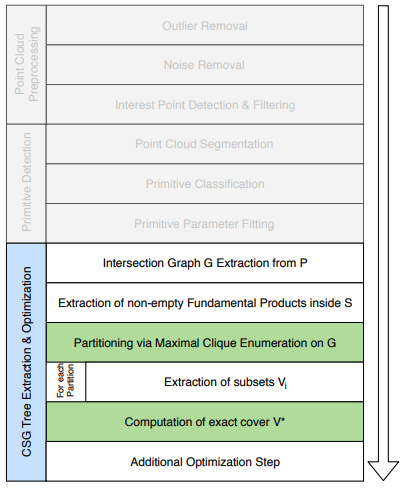
The full CSG tree extraction pipeline — CSG木を作るためのパイプライン

この論文ではポイントクラウドを作成するための前処理部分と基本構成要素決定の部分は考えず、灰色で覆っています。CSG木の抽出と最適化の部分(青色)が本論文で議論する部分、そして量子アニーリングハードウェアで最適化を実行できる部分をさらに緑色で塗り分けています。

CSG木の抽出問題

最適化問題としてのCSG木抽出

基本構成要素Pが既知であるときに、木の幾何(大きさ、ノード・辺の構造)を見つけ、その木 $\Phi(P)$ が目的としている物体表面Sとなるように最適化せよ、というものです。

考えられる戦略としてはCSG木の最大サイズを決め、全ての木の組み合わせに対して、木のサイズが大きければペナルティを与えるかつ入力点群に対して表面Sからの誤差を最小化するようなコストを考えて定式化する方法があります。

組み合わせが膨大な数になってしまいますが、これは基本構成要素同士の関係性から緩めることが可能です(例えばある2つの要素は共通部分を持たないので、木においてもブーリアン演算をする必要がなくなる、など)。選ぶソルバーに依存しますが、この方法ならば確実に最小木を得ることができます。しかし。10以下の基本要素からなる物体表面でも高コストの計算が必要となることがあります。

CSG木の制約

組み合わせが膨大になってしまうことに対しての解決方法の一つをご紹介いたします。それは、基本構成要素の共通部分を元に(これを基本生成物と呼びます)、それらの和として木の幾何構造を限定するDCF(Disjunctive Canonical Form, 分離的カノニカル形式)の類型と呼べるものです。数式で表すと

$\displaystyle{ \Phi (P) = \bigcup^{2|P|-1}_{k=1} g_1 \cap g_2 \cap \cdots \cap g_{|P|} \ (g_i \in \{ p_i, \bar{p_i}\}) }$

のようになります。例として全て円からなる表面S(灰色)を下左図(a)に示しました。

基本構成要素 $P = \{ A, B, C, D, E, F\}$ から表面Sを作ります。1-15の番号がこの基本構成要素からできる基本構成物です。
この図形をG(P, I)のように表します。Pは構成要素、Iは $(p_i, p_j)$ を結ぶ辺の集合です。
すると上右図(b)のように、(a)に対応するグラフGを表現することができます。辺はその要素同士が共通部分を持っていることを表します。最大クリークのセットとしてQ = { {A, B}, {B, C, D}, {B, D, E}, {E, F} }が含まれています。
上図の表面Sを作成するには{1, 2, 3, 4, 7, 8, 10, 13}の基本生成物を用いれば良いです。これを作る木の表現としては $(A \cap \bar{B}) \cup (A \cap B) \cup (\bar{A} \cap B \cap \bar{C} \cap \bar{D} \cap \bar{E}) \cup (B \cap \bar{D} \cap E) \cup (B \cap C \cap D) \cup (B \cap C \cap \bar{D}) \cup (\bar{B} \cap C \cap D) \cup (\bar{B} \cap \bar{D} \cap E \cap F)$ のように、クリークの共通部分の和集合として表すことができます。しかし最小木としてはこれよりも70%も小さい $A \cup (B\cap \bar{D}) \cup (C \cap D) \cup (\bar{D} \cap E \cap \bar{F})$ が存在するため、これを今度は最適化する必要があります。

CSG木のサイズ最適化

よって次の問題としてはどのように小さいCSG木へと改良を行うか、です。上図の例で例えると{7, 10}の基本生成物は $C\cap D$ と表現できるにもかかわらず、 $(B \cap C \cap D) \cup (\bar{B} \cap C \cap D)$ のように計算しています。

これを解消するために以下のように考えます。基本生成物の数を $n_f \in [|P|, 2^{|P|}-1$ ]とします。すると木のサイズを小さくする問題は基本生成物の番号とする最小被覆問題に帰着することができます(例えば7はB, C, Dの共通部分、10はC, Dの共通部分で、この7と10をカバーするにはC, Dの二つだけで十分ということ)。この問題はNP完全であることが知られています。

問題分割

クリークに分割し、問題サイズを小さくしてからこれを解き、それらを組み合わせることで問題を解くという手法を用いています。そのため、これは本当の最適解でないことがあります。例えば先ほどの図で一番良い答えは $A \cup (B\cap \bar{D}) \cup (C \cap D) \cup (\bar{D} \cap E \cap \bar{F})$ としましたが、我々のアプローチだと $(A \cap \bar{B}) \cup (B \cap \bar{D}) \cup (C\cap D)\cup (\bar{B} \cap \bar{D} \cap E \cap \bar{F})$ となり、少し大きな木になっています。