量子アニーリングによる衛星写真撮影計画の最適化

この記事の概要

2020 Jun. 17 にarXivに投稿されたStollenwerk et al. "Image Acquisition Planning for Earth Observation Satellites with a Quantum Annealer"を読んだので、その解説をいたします。

この記事の概要
本論文の概要
問題詳細
インスタンス
量子アニーリング
- QUBO
- 未定乗数
量子アニーリングと古典アルゴリズムの比較
- Time-to-exact-solution ベンチマーク
- 解の質についてのベンチマーク
結言
参考文献
文責

本論文の概要

D-Waveマシンを用いて衛星画像撮影スケジュールの最適化を行い、そのベンチマークを取得しました。

問題詳細

問題概要

地球上のある位置を衛星から撮影するには、その方向に衛星カメラを指向する必要があります。衛星は常に動き続けているため、衛星が地球上のある位置を撮影するには限られた角度で撮影をする必要があります。また衛星自身の姿勢を制御する時間が取られてしまうため、撮影する順序を慎重に選ばなければ目標とする収益(ここでの収益とは衛星写真を撮影することでクライアントから得られる支払い)を達成できません。

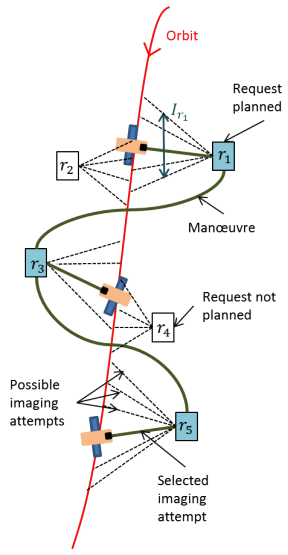
Illustration of a mission plan — 衛星軌道と衛星写真を撮影したいエリアのイラスト。

論文では以下のような変数を考えています。

$R$ : 観測できるエリアの中で撮影リクエストがきたエリアのセット
$I_r$ : 撮影するエリア $r \in R$ において、そのエリアが撮影できる軌道上の範囲
$w_{r, i}$ : 撮影範囲 $i \in I_r$ にエリア $r$ を撮影したことによって得られる金額のスコア(大体においては軌道上のどの位置から撮影してもスコアに変動がないので $w_{r, i} \rightarrow w_r$ とすることもあります)
$t_i^r$ : 衛星写真撮影を $i$ で行おうとしたときの、撮影開始時刻
$d_{r, i}^{\rm acq}$ : $i$ での撮影に要する時間
$d_{(r, i) \rightarrow (s, j)}^{\rm man}$ : $i \in I_r$ から次の軌道上の位置 $j\in I_s$ でエリア $s$ の写真撮影を行うために、姿勢制御に必要な時間

数理モデル化

バイナリ変数

衛星からエリア $r$ を軌道上の位置 $i$ で撮影できたときを1, それ以外を0とするようなバイナリ変数 $x_{r, i}$ を定義します。

コスト

上述の通り、クライアントの希望通りに撮影できたエリアの数とそのエリア撮影の見返りとしていくら報酬がもらえるのかを盛り込む必要があります。よって最大化したいコスト関数は

$\displaystyle{ \sum_{r \in R} \sum_{i \in I_r} w_{r, i} x_{r, i} }$

となります。

制約

1. 軌道上の位置において、あるエリアを撮影できる回数は1回以下でなければならない

任意の位置からあるエリアを撮影できるのは一度きりです。ただし撮影しないという選択肢もあるので、これを数理モデルに組み込みます。

$\displaystyle{ \sum_{i \in I_r} x_{r, i} \leq 1 \ (\forall r \in R) }$

2. 姿勢制御中に撮影はできない

ある一つのエリアを撮影し終わったとしましょう。次の撮影エリアの方角を向くためには姿勢制御の時間が必要です。その間はそもそもそちらの方角を向けていないことや、撮影の前準備などの時間が取られるために撮影ができません。

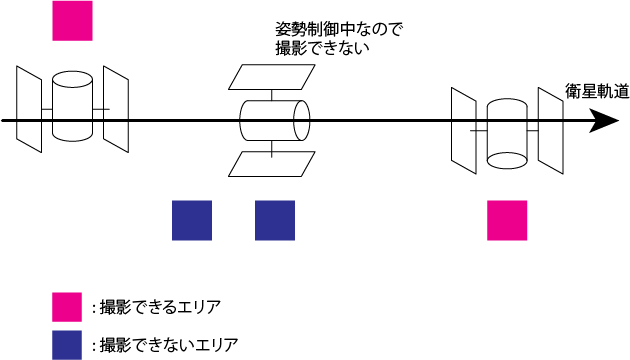
Illustration of direction and detectable area. — 衛星の向いている方向と撮影できるエリアの図

よって衛星軌道上の位置 $i$ で撮影できたエリア $r$ と、次の衛星軌道上の位置 $j \in I_s$ で撮影するエリア $s$ には許されない組みが存在することがわかります。これを数理モデルにすると以下のようになります。

$\displaystyle{ x_{r, i} + x_{s, j} \leq 1 \ (\forall (i, j) \in F_{r, s}, \ \forall (r, s) \in R^2, \ r\neq s) }$

ここで $F_{r, s}$ は

$\displaystyle{ F_{r, s} = \{(i, j) \in I_r \times I_s: t_i^r \leq t_j^s < t_i^r + d_{r, i}^{\rm acq} + d_{(r, i) \rightarrow (s, j)}^{\rm man}\} }$

のように、 $(i, r)$ の撮影を行なった場合に撮影が許されないペアの集合です。

最適化問題としての衛星写真問題

数理モデルから、解きたい問題を整理すると以下のようになります。

$\displaystyle{ \begin{array}{l} {\rm min} & - \sum_{r \in R} \sum_{i \in I_r} w_{r, i} x_{r, i} \\ {\rm s. t.} &\sum_{i\in I_r} x_{r, i} \leq 1 \ (\forall r \in R) \\ &x_{r, i} + x_{s, j} \leq 1 \ (\forall (i, j) \in F_{r, s}, \ \forall (r, s) \in R^2, \ r\neq s) \\ &x_{r, i } \in \{0, 1\} \ (\forall i \in I_r, \forall r \in R) \end{array} }$

この問題は整数線形計画問題なので、これは一般にはNP困難です。

インスタンス

現実の衛星画像取得のようなインスタンスを組む必要があります。そのために

クライアントから撮影してほしいエリアの総数を $N_R = |R|$
２つの写真を撮影に必要な時間の長さ $\Delta t$ で離散化
軌道から $[-\Lambda: \Lambda$ ]の範囲からランダムに撮影エリアを抽出

とします。さらに組まれたインスタンスがどの程度難しい問題であるかを以下の量を用いて検討します。

バイナリ変数の総数 $N = \sum_{r\in R} |I_r|$
制約率 (%) $n_C = 100 \frac{2 N_C}{N(N-1)}$

ここで

$\displaystyle{ N_C = \sum_{s, r\in R \\ s\neq r} |F_{r, s}| + \sum_{r\in R} \frac{1}{2} |I_r| (|I_r| -1) }$

は禁止ペアの数であり、 $\frac{1}{2} N(N-1)$ は全組み合わせの数です。

量子アニーリング

QUBO

Total QUBOコストは

$\displaystyle{ Q = C + \lambda_u C_u + \lambda_t C_t }$

と書けます。ここでCはコスト $\sum_{i \in I_r} x_{r, i} \leq 1 \ (\forall r \in R)$ 、そして $C_u$ は

$\displaystyle{ C_u = \sum_{r\in R} \sum_{j \in I_r\\ i\neq j} x_{r, i} x_{r, j} }$

同様に $C_t$ は

$\displaystyle{ C_t = \sum_{r, s \in R \\ r\neq s} \sum_{(i, j) \in F_{r, s}} x_{r, i} x_{s, j} }$

となります。

未定乗数

コスト項と制約項が同等の大きさに定めなくては、正しく最適化が行われません。よってコストがおよそ

$\displaystyle{ \bar{\lambda} = \max_{r\in R \\ i \in I_r} w_{r, i} }$

程度の大きさと見積もって、論文では未定乗数の大きさを

$\displaystyle{ \lambda_u = \lambda_t = 1.1 \bar{\lambda} }$

としています。

量子アニーリングと古典アルゴリズムの比較

Time-to-exact-solution ベンチマーク

量子アニーリング(QA)ではD-Waveマシンを用います。そのときのアニーリング時間を $T_{\rm Anneal} = 20{\rm \mu s}$ として、99%の成功確率で厳密解を得られるのにかかる時間は

$\displaystyle{ T_{99} = \frac{\ln (1-0.99)}{\ln (1-p)}T_{\rm Anneal} }$

となります。これを用いてQAと古典アルゴリズムを比較しています。

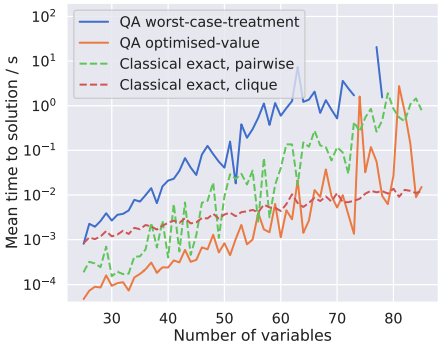
TTS comparison of classical exact solver and QA. — TTSの比較。

チューニングされたQA(オレンジ線)は異なる二つの古典ソルバー(緑破線と赤破線)よりも良く解けていることがわかります。

65以上のインスタンスでは問題が急激に難しくなるため、そもそも最適解がもとまらないことが多くなります。よって65以下の問題サイズのインスタンスの部分のみ信頼できるデータと言えるでしょう。

解の質についてのベンチマーク

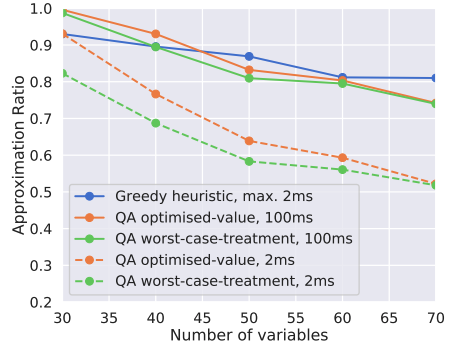
Classical greedy heuristic vs QA for quality of solution with fixed time. — 計算時間を固定したときの、得られる解の性質を比較したもの。

上図はインスタンスとして難しいものを選び、そして計算時間を固定した場合に、横軸の問題サイズに対して縦軸を最適解を得られる率でプロットしたものです。例えばQA optimised-value, 100msは最適化されたチェインカップリング係数 $J_C$ に対して、100msの間にアニーリング計算を繰り返して得られたプロットです。貪欲法で2msの計算時間を与えられたものと同等の解を出すためには、QAでは100msの計算時間が必要ということになります。