量子アニーリングを用いたエネルギーギャップの直接測定法

本記事の概要

2020年7月21日にアーカイブに投稿された論文Matsuzaki et al. "Direct estimation of the energy gap between the ground state and excited state with quantum annealing"について、その内容をまとめました。

本記事の概要
論文概要
ラムゼー型の測定による基底状態と励起状態のエネルギーギャップの測定
実験
結言
参考文献
文責

論文概要

これまでの方法は基底状態と励起状態を別々に求めて、その差からエネルギーギャップの大きさを見積もっていました。本論文では量子アニーリングを用いて、ターゲットとしているハミルトニアンのエネルギーギャップを直接求める方法をご紹介します。鍵となるアイデアはラムゼー型の測定と量子アニーリングの組み合わせです。

ラムゼー型の測定による基底状態と励起状態のエネルギーギャップの測定

以下の時間依存ハミルトニアンを用います。

$\displaystyle{ H = A(t) H_D + (1- A(t)) H_P }$

ここで $H_D$ はDriving Hamiltonian (代表的なものは横磁場イジングの量子項)、 $H_P$ は解きたい問題のハミルトニアン(ターゲットハミルトニアン)です。そして $A(t)$ は

$\displaystyle{ A(t) = \left\{ \begin{array}{ll} 1-\frac{t}{T} & (0 \leq t \leq T) \\ 0 & (T \leq t \leq T+\tau) \\ \frac{t-(T+\tau)}{T} & (T+\tau \leq t \leq 2T + \tau) \end{array} \right. }$

というスケジュールを表す関数です。このことから、この論文では以下のようにハミルトニアンを3段階に使い分けていることがわかります。

$\displaystyle{ H_{\rm QA} = (1-\frac{t}{T}) H_D + \frac{t}{T} H_P \\ H_{\rm R} = H_P \\ H_{\rm RQA} = \frac{t-(T+\tau)}{T} H_D + (1-\frac{t-(T+\tau)}{T}) H_P }$

$H_{\rm QA}$ は通常のアニーリング、 $H_{\rm R}$ はラムゼー型測定のようにアニーリングを停止して状態を発展させることに対応し、 $H_{\rm RQA}$ はリバース・アニーリングをしていることがわかります。

第一ステップ: 初期状態

これによってどのようにエネルギーギャップを測定するのかを説明するために、初期状態として $\left| \psi_0 \right\rangle = \frac{1}{\sqrt{2}} (\left| E_0^{(D)} \right\rangle + \left| E_1^{(D)} \right\rangle)$ を選択します。ここで $\left| E_0^{(D)} \right\rangle, \left| E_1^{(D)} \right\rangle$ はそれぞれ $H_D$ における基底状態と励起状態です。

第二ステップ: 量子アニーリング

次に断熱的に $H_{\rm QA}$ にしたがって状態を変化させることにより $\frac{1}{\sqrt{2}} (\left| E_0^{(P)} \right\rangle + e^{-i\theta}\left| E_1^{(P)} \right\rangle)$ を得ます。ここで $\left| E_0^{(P)} \right\rangle, \left| E_1^{(P)} \right\rangle$ はそれぞれ $H_P$ における基底状態と励起状態であり、 $\theta$ はダイナミクスにより変化した相対的な位相です。

第三ステップ: ラムゼー型測定(アニーリング停止)

続いて $H_{\rm R}$ にしたがって状態を変化させます。これは $\tau$ だけ状態を停止させる操作になるので、状態は

$\displaystyle{ \frac{1}{\sqrt{2}} (\left| E_0^{(P)} \right\rangle + e^{-i\Delta E \tau - i\theta} \left| E_1^{(P)} \right\rangle ) }$

のようになります。ここで $\Delta E$ は基底状態と励起状態のエネルギーギャップです。

第四ステップ: リバース・アニーリング

断熱的に $H_{\rm RQA}$ にしたがって状態を変化させます。最終的に得られる状態は

$\displaystyle{ \frac{1}{\sqrt{2}} (\left| E_0^{(D)} \right\rangle + e^{-i\Delta E \tau - i\theta'} \left| E_1^{(D)} \right\rangle ) }$

となります。ダイナミクスによって変化した位相を $\theta'$ のように書きます。

第五ステップ: 結果の読み出し

射影演算子 $\left| \psi_0 \right\rangle \left\langle \psi_0 \right|$ を用いて結果を読み出します。射影測定により得られる確率は

$\displaystyle{ P_\tau = \frac{1}{2} + \frac{1}{2} \cos (\Delta E \tau + \theta') }$

となります。

最終ステップ: 繰り返しとフーリエ変換

以上のステップを異なる $\tau$ ごとに繰り返します。得られた $P_\tau$ をフーリエ変換します。

$\displaystyle{ f(\omega) = \int_{-\infty}^\infty (P_\tau - \frac{1}{2}) e^{-i\omega \tau} d\tau \propto \delta (\omega - \Delta E) }$

すると関数 $f(\omega)$ は $\omega \simeq \Delta E$ でピークを持つような関数になります。これにより基底状態と励起状態を求めることなく、 $\Delta E$ を求めることができます。

実験

論文ではこの手法がどれだけ有用かを確かめるための数値実験を行なっています。用いたハミルトニアンは

$\displaystyle{ H_D = \sum_{j=1}^L \frac{\lambda_j}{2} \hat{\sigma}_x^{(j)} \\ H_P = \sum_{j=1}^L \frac{\omega_j}{2} \hat{\sigma}_z^{(j)} + \sum_{j=1}^{L-1} g\hat{\sigma}_z^{(j)} \hat{\sigma}_z^{(j+1)} + g' (\hat{\sigma}_+^{(j)}\hat{\sigma}_-^{(j+1)} + \hat{\sigma}_-^{(j)}\hat{\sigma}_+^{(j+1)}) }$

のようなものです。以下にその数値実験結果を示します。

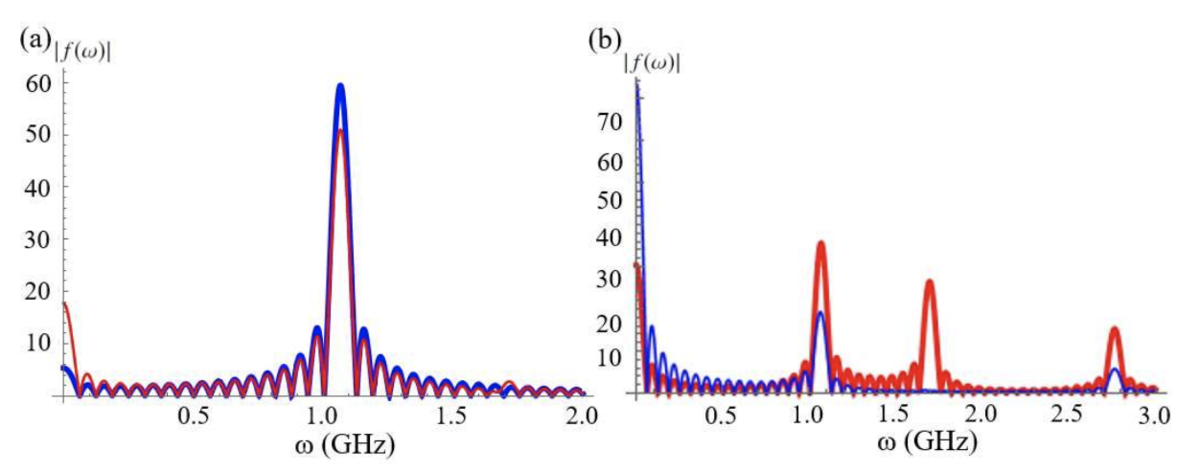
Fourier function against a frequency — 横軸: 振動数、縦軸: 測定結果をフーリエ変換したもの。

左の図において青線が $T=150$ ns, 赤線が $T=75$ nsでの実験結果です。どちらの場合にも $\omega \sim 1.067$ GHzにピークを持っています。
右の図は青線が $T=37.5$ ns, 赤線が $T=12.5$ nsでの結果です。青線の $\omega=0$ のピークは非断熱遷移によるものです。そして赤線のいくつかのピークは基底状態や第一励起状態と第二励起状態のエネルギーギャップを表しています。