この記事の概要
この記事はShuld et al., 2017, "Implementing a distance-based classifier with a quantum interference circuit"を読んだので、その理解を深めるためのアウトプットとして作成したものです。
距離に基づいた分類器
教師データセットがのように
個のデータ点からなるとします。それぞれのデータ点は
次元であるとします(
)。
は分類を表すラベルです。これに対してラベルが割り振られていない入力データ
のラベル
を付与することを目標とします。
閾値と分類モデル
分類を量子回路で行うにあたり、以下の閾値関数を用います。
距離指標
をカーネルとして扱います。このカーネルはEpanechnikovカーネル
に類似しています。この類似性から、(1)式はカーネル化したバイナリ分類
においてとしたものに等しいことがわかります。このような式はパーセプトロンから導かれるモデルで、
とした重みが学習データの拡張を表現していることがRepresenter theoremからわかります。
教師データと入力データの標準化と規格化
この論文ではIrisデータセットを用いて数値実験を行っています。その際に、予めデータの標準化と規格化を行っています。
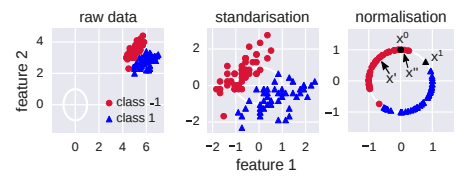
左図は生データです。真ん中図は標準化し、平均0, 分散1にしたものです。右図は各データ点を原点から長さ1の場所に規格化したものです。
用いる量子ビットとその役割
距離指標を用いた分類器を量子回路で実現するには4種類の量子ビットを用います。
最初のは教師データのインデックスを表す量子ビット、2つ目の
は分類したい入力データ
と教師データ
とにエンタングルさせておくための単一の補助量子ビット、3つ目の
はすでに説明した通りそれぞれ入力データと教師データを表す量子ビット、そして最後の
は
番目の教師データがどちらの分類されているかを表す単一の量子ビットです。
ここで
であり、は次元のインデックスを表すベクトルです。
考え方
最初に、2つ目の補助量子ビットにアダマールゲートを作用させてみましょう。
この状態において補助量子ビットがとなる状態を測定したとき、それが測定される確率は
となります。この測定後の他の量子ビットの状態は
になります。この状態において最後の量子ビットを測定したとき、
が測定される確率は
となります。これがラベル-1に分類される確率になります。よって途中で出てきたをデータ前処理で高めることにより、正しく分類できるようになります。
数値実験
教師データと分類したい入力データ
教師データとして
の2つを用います。そして分類したい入力データには
を用います。
量子回路
以下に、先ほどの教師データと分類したい入力データを用いた場合の量子回路を示します。

上から順に
: 補助量子ビット
: 教師データのインデックスを表す量子ビット
: 教師データと入力データを表す量子ビット
: 分類を表す量子ビット
です。では量子回路の各工程を見てみましょう。
step A: 補助量子ビットとインデックス量子ビットにアダマールゲートを作用させます。
step B: 入力データの偏角2.152の倍の角度の位相回転を行い、これと補助量子ビットの基底状態
をエンタングル状態にします。
step C: 教師データと補助量子ビットの励起状態
及びインデックス量子ビットの基底状態をエンタングル状態にします。
step D: 教師データの偏角0.662の倍の角度の位相回転を行い、これと補助量子ビットの励起状態
とインデックス量子ビットの励起状態をエンタングル状態にします。
step E: データ量子ビットと分類量子ビットをスワップし、さらに分類量子ビットをインデックス量子ビットのを用いてフリップします。
step F: 補助量子ビットにアダマールゲートを作用させ、補助量子ビットがの状態を測定します。その後、分類量子ビットを測定し、分類確率を得ます。
step A-Eまでは先ほど説明したを作成し、step Fで確率の測定を行います。
数値実験結果
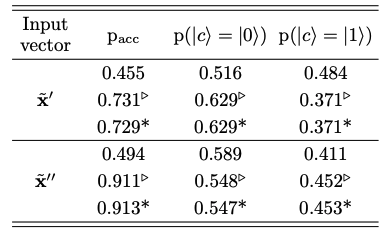
上の表は無印がIBM Quantum Experience実機での結果、三角がシミュレーションによる結果、そしてアスタリスクが理論予想です。理論予想とシミュレーション結果は近しい値を示していますが、実機での結果は大きく外れた値が出ています。この主な理由として、エラー補正がないこと、補助量子ビットの横方向コヒーレンス時間が短いために初期の一様な重ね合わせが崩れてしまったこと、そして分類量子ビットの縦方向コヒーレンス時間が短いことがあります。
様々なタイプのデータセットでの実験
この距離指標に基づいた分類器がどのような分布のデータでも有用なのかを調べるために、様々な分布のデータセットの分類でシミュレーションを行っています。

Circlesデータセットでは正しく分類できていないことがわかります。
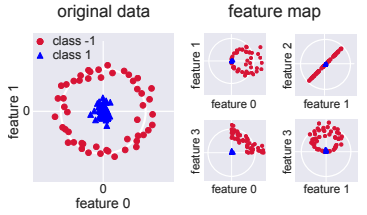
上左図がCirclesデータセットです。このままでは正しく分類することができません。しかし上右図のような特徴量ベクトルを表す量子状態のコピーを用いることで、分類器の力を向上させる多項式特徴量マップを実装することも可能です。
結言
今回は数ある分類器の中でも、距離指標に基づいた分類器とその量子回路実装をご紹介しました。