量子回路でK-Meansクラスタリング

この記事の概要

2019年9月にarXivに投稿された論文、Khan et al., "K-Means Clustering on Noisy Intermediate Scale Quantum Computers"を読むための前提知識を学習するために作成した記事です。

この記事の概要
序章: K-Means法
- アルゴリズム
- 計算量
量子K-Means法
結言
参考文献
文責

序章: K-Means法

アルゴリズム

与えられたデータをいくつかのグループにグループ分けすることをクラスタリングと呼びます。ここでは数あるクラスタリングアルゴリズムの中から、基本的なものであるK-Means法を復習しましょう。
以下のように与えられたデータを5つのグループにクラスタリングします。

この図上に5つの色付き点をランダムに配置します。

points of data and color points — データ点と色付き点

各点から一番近い色付き点を線で繋ぎます。どの点がどの色付き点と線で結ばれているか、わかりやすくするために色で塗り分けしてあります。

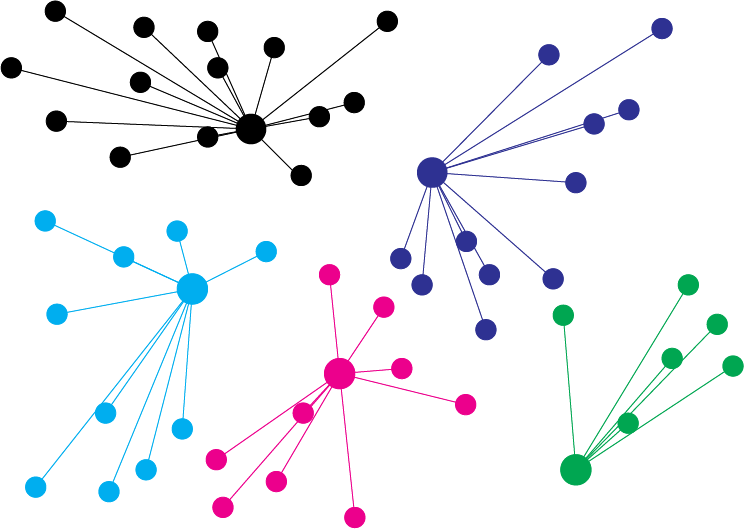
connect with data points and nearest color points — データ点と最も近い色付き点を結ぶ

次に、各色付き点を自分の色のついているデータ点の重心に移動させます。

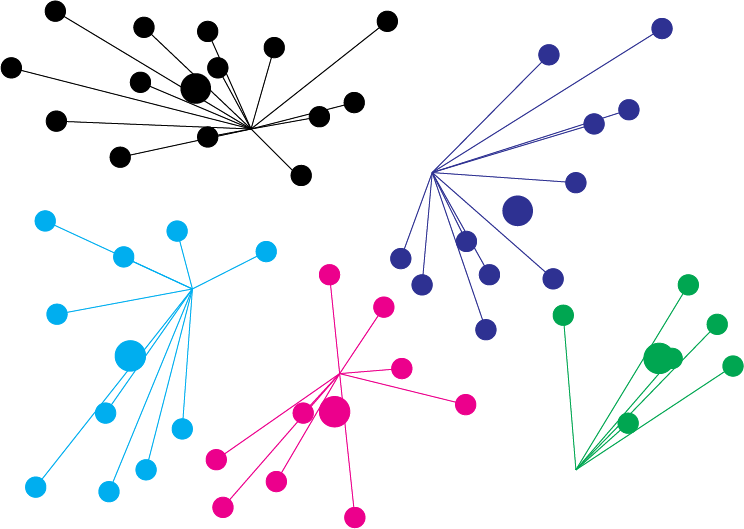
色付き点が移動したため、各データ点からの距離が変わりました。そこで、再び各データ点から一番近い色付き点を線で繋ぎ直しましょう。それに伴って、いくつかのデータ点の色も変わります。

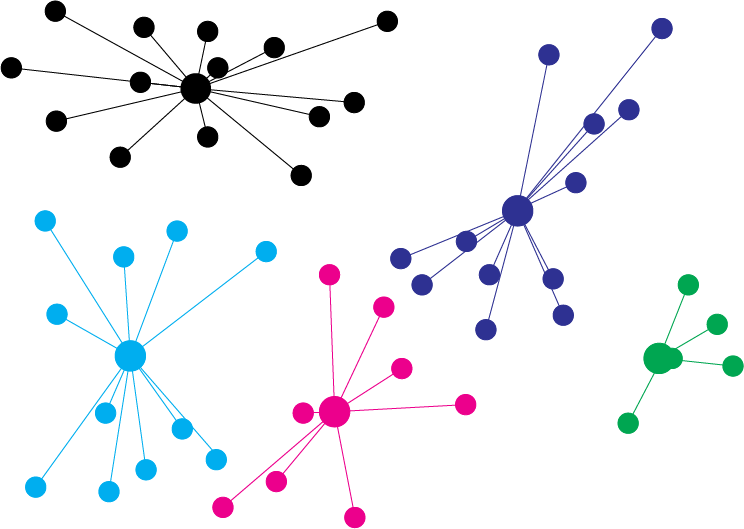
again, connect data points with nearest color points — 再びデータ点と色付き点を結ぶ

再び各色付き点を自分の色のついているデータ点の重心に移動させ、さらにデータ点から一番近い色付き点を線で繋ぎ直します。

この操作を色付き点が移動しなくなるまで繰り返します。これにより与えられたデータ点を5つにグループ分けできます。これをK-Means法と呼びます。
K-Means法はそのアルゴリズムの性質上、色付き点の初期位置によって結果が大きく変わります。またデータによって直感と反する結果になることも多々あります。

計算量

入力データの特徴量の数(次元数)を $N$ , 入力データ数を $M$ , そしてクラスタリング数を $K$ とすると、計算時間は $\mathcal{O}(MNK)$ となります。

量子K-Means法

量子K-Meansのアルゴリズムの流れを以下に示します。

量子状態の準備

以下の二つの量子状態を準備します。

$\displaystyle{ | \psi \rangle = \frac{1}{\sqrt{2}} (| 0, a \rangle + | 1, b \rangle ) \\ | \phi \rangle = \frac{1}{\sqrt{Z}} (|a| | 0 \rangle + |b| | 1 \rangle ), \ (Z = |a|^2 + |b|^2) }$

オーバーラップの計算

Swap Testを用いて、オーバーラップ $\langle \psi | \phi \rangle$ を計算します。

Swap Test

1. Controlled-swap

Swap Testの量子回路を考える前に、Controlled-swap(別名フレドキンゲート)と呼ばれる以下のようなものを考えます。

$\displaystyle{ \left( \begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right) }$

controlled-swapは一つ目の量子ビットが状態1であれば、残りの2つの状態を入れ替えます。

量子回路

Swap Testの量子回路をご説明します。

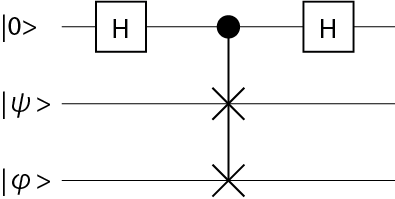
上のHはアダマールゲート、そして真ん中の量子ゲートは先ほど説明したcontrolled-swapゲートです。それではこの回路の挙動を見ていきましょう。最初に一つ目の量子ビットにアダマールゲートを作用させるので

$\displaystyle{ |0 \rangle \otimes |\psi \rangle \otimes |\phi \rangle \longrightarrow \frac{1}{\sqrt{2}} (|0 \rangle + | 1 \rangle ) \otimes | \psi \rangle \otimes | \phi \rangle }$

となります。次にcontrolled-swapによって、一つ目の量子ビットが状態1であれば2つ目と3つ目の状態を交換します。

$\displaystyle{ \frac{1}{\sqrt{2}} (|0 \rangle \otimes | \psi \rangle \otimes | \phi \rangle + |1 \rangle \otimes | \phi \rangle \otimes | \psi \rangle ) }$

さらに一つ目の量子ビットにアダマールゲートを作用させます。

$\displaystyle{ \frac{1}{2} (|0 \rangle + |1 \rangle ) \otimes |\psi \rangle \otimes |\phi \rangle + \frac{1}{2} (|0 \rangle - |1 \rangle ) \otimes |\phi \rangle \otimes |\psi \rangle = \frac{1}{2} | 0 \rangle \otimes (|\psi \rangle \otimes |\phi \rangle + |\phi \rangle \otimes |\psi \rangle) + \frac{1}{2} |1 \rangle \otimes (|\psi \rangle \otimes |\phi \rangle - |\phi \rangle \otimes |\psi \rangle) }$

最後に1番目の量子ビットを観測し、 $| 0 \rangle$ を得る確率を求めます。この場合の測定演算子は $| 0 \rangle \langle 0 | \otimes I \otimes I$ と書けるので

$\displaystyle{ \begin{align} &\left| ( | 0 \rangle \langle 0 | \otimes I \otimes I ) \left\{ \frac{1}{2} | 0 \rangle \otimes (|\psi \rangle \otimes |\phi \rangle + |\phi \rangle \otimes |\psi \rangle) + \frac{1}{2} |1 \rangle \otimes ( \cdots ) \right\} \right|^2 \\ &= \frac{1}{4} \left\{ \langle 0 | \otimes (\langle \psi | \otimes \langle \phi | + \langle \phi | \otimes \langle \psi | ) + \langle 1 | \otimes (\cdots) \right\} (| 0 \rangle \langle 0 | \otimes I \otimes I ) \left\{ | 0 \rangle \otimes (| \psi \rangle \otimes | \phi \rangle + | \phi \rangle \otimes | \psi \rangle ) + | 1 \rangle \otimes (\cdots) \right\} \\ &= \frac{1}{4} \langle 0 | 0 \rangle \langle 0 | 0 \rangle ( \langle \psi | \psi \rangle \langle \phi | \phi \rangle + \langle \psi | \phi \rangle \langle \phi | \psi \rangle + \langle \phi | \psi \rangle \langle \psi | \phi \rangle + \langle \phi | \phi \rangle \langle \psi | \psi \rangle ) \\ &= \frac{1}{2} (1 + |\langle \phi | \psi \rangle |^2) \end{align} }$