Adiabatic PageRank algorithm

この記事の概要

Googleのページ検索において重要な技術にページランクアルゴリズムがあります。この記事はその概要と、そのページランクを断熱量子計算で高速に求める手法をご紹介します。

この記事の概要
Google行列
断熱量子計算
- ハミルトニアンとエネルギーギャップ
  - ハミルトニアン
  - エネルギーギャップとアニーリング時間
- 古典と比べてどのくらい高速化したか？
結言
参考文献
文責

Google行列

ページ間リンク

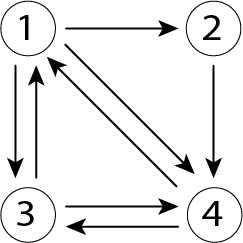
上図ように、ページ1からはページ2, 3, 4へのリンク、ページ2からはページ4へのリンク、ページ3からはページ1, 4へのリンク、そしてページ4からはページ1, 3へのリンクがそれぞれ貼られているとします。このときどのページが重要度が高いでしょうか、というのがページランクアルゴリズムで求めたい答えです。

このとき

(1, 2), (1, 3), (1, 4)の3本をエッジとして持つ => d(1) = 3
(2, 4)の1本をエッジとして持つ => d(2) = 1
(3, 1), (3, 4)の2本をエッジとして持つ => d(3) = 2
(4, 1), (4, 3)の2本をエッジとして持つ => d(2) = 2

よりこのリンク情報を以下のようにページ数xページ数の隣接行列で表現します。

$\displaystyle{ P_1 (i, j) = \left( \begin{array}{cccc} 0 & 1/3 & 1/3 & 1/3 \\ 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 1/2 \\ 1/2 & 0 & 1/2 & 0 \end{array} \right) }$

より一般的に記述すると $P_1 (i, j)$ は以下のようになります。

$\displaystyle{ P_1 (i, j ) = \left\{ \begin{array}{ll} 1/d(i) & {\rm if \ there \ is \ a \ link \ from } \ i \ {\rm to} \ j \\ 0 & {\rm otherwise} \end{array} \right. }$

イテレーションによるページランクベクトルの計算

初期に全てのページの重要度が等しく ${\bf p}_0 = (1/4, 1/4, 1/4, 1/4)$ としましょう。これをページランクベクトルと呼びます。ここに隣接行列 $P_1^T$ をかけることで、そのページがどの程度他のページと関わりがあり重要であるかがわかります。これを繰り返し作用させることで値が収束し、最終的なページ重要度を得ることができます。

$\displaystyle{ {\bf p} = \lim_{k\rightarrow \infty} (P_1^T)^k {\bf p}_0 }$

ここで $T$ は行列の転置を表します。実際に上の例でこれを計算すると以下のように値が収束していきます。

iteration回数	1	2	3	4
0	0.25	0.25	0.25	0.25
5	0.299	0.100	0.267	0.332
10	0.3	0.1	0.266	0.333

よってこの例ではページ4が最も重要であることがわかります。これは他のページに比べて、ページ4に入ってくるリンクの数が3つで一番多いことに起因しています。

ぶら下がりページ(dangling nodes)の扱い方

下図のページ4のように、他のページからリンクが貼られていてもそこから先にはページが貼られていないようなページのことをぶら下がりページと呼びます。

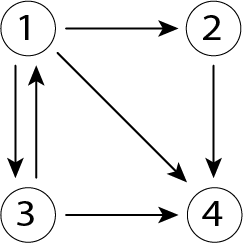
A example of dangling nodes — ぶら下がりページがある例

上述の議論からこのグラフの隣接行列は

$\displaystyle{ P_1 (i, j) = \left( \begin{array}{cccc} 0 & 1/3 & 1/3 & 1/3 \\ 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 1/2 \\ 0 & 0 & 0 & 0 \end{array} \right) }$

となります。これを用いて繰り返し計算を行ってみましょう。すると

iteration回数	1	2	3	4
0	0.25	0.25	0.25	0.25
5	0.001	0.001	0.001	0.004

のように全ての成分が0に収束するようになり、正しくページランクベクトルを計算することができません。よってこれを回避するために、ある行の成分が全て0の場合はページ数分の1、すなわち $1/n$ を代わりに入力します。この行列を $P_2$ とすると

$\displaystyle{ P_2 (i, j) = \left( \begin{array}{cccc} 0 & 1/3 & 1/3 & 1/3 \\ 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 1/2 \\ 1/4 & 1/4 & 1/4 & 1/4 \end{array} \right) }$

このとき

$\displaystyle{ {\bf p} = \lim_{k\rightarrow \infty} (P_2^T)^k {\bf p}_0 }$

の値の収束を見てみましょう。

iteration回数	1	2	3	4
0	0.25	0.25	0.25	0.25
5	0.200	0.178	0.178	0.442
30	0.2	0.177	0.177	0.444

のようになりました。このことから3ページからリンクが貼られているページ4が最も重要であることがわかります。

可約グラフがある場合とGoogle行列

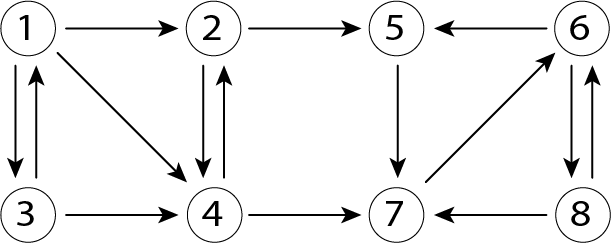
上図のようなグラフの場合、リンクの情報を表す隣接行列は以下のようになります。

$\displaystyle{ P_2 (i, j) = \left( \begin{array}{cccccccc} 0 & 1/3 & 1/3 & 1/3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1/2 & 1/2 & 0 & 0 & 0 \\ 1/2 & 0 & 0 & 1/2 & 0 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 0 & 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1/2 & 0 & 0 & 1/2 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1/2 & 1/2 & 0 \end{array} \right) }$

しかし実際のこれを使って繰り返し計算を行ってページランクベクトルを計算すると

iteration回数	1	2	3	4	5	6	7	8
0	0.125	0.125	0.125	0.125	0.125	0.125	0.125	0.125
30	0.000	0.000	0.000	0.000	0.102	0.364	0.273	0.182

のように、1~4までの重要度が0に収束します。元のグラフをみてみると、ページ4はページ1, 2, 3からリンクされているため、本来ならば0でない重要度になってほしいところです。
この例は実は可約グラフ(reducible graph)になっており、このままではページランクベクトルを正しく計算することはできません。

そこでBrin & Page 1998では以下のように隣接行列に修正を加え、これをGoogle行列と定義しました。

$\displaystyle{ G : = \alpha P_2^T + (1-\alpha) E }$

ここで $E = | {\bf v} \rangle \langle {\bf e} |$ です。 ${\bf v}$ は"Personalization vector"と呼ばれる確率分布を表します。よく用いられるのは、全ての分布を等しく $1/n$ としたものです。 ${\bf e}$ は全ての要素が1のベクトルです。 $\alpha$ は、グラフにしたがって別のページへと遷移する確率を表すパラメータです。すなわちこの式は ${\bf v}$ の確率分布にしたがって、 $1-\alpha$ 程度はランダムなページ遷移を許容することを意味します(Googleが用いている値は $\alpha = 0.85$ )。

簡単のため、上述のよく用いられる例でGoogle行列を書き直してみましょう。

$\displaystyle{ G = 0.85 P_2^T + \frac{0.15}{8} \left( \begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array} \right) }$

これを用いてページランクベクトルの収束をみてみましょう。

iteration回数	1	2	3	4	5	6	7	8
0	0.125	0.125	0.125	0.125	0.125	0.125	0.125	0.125
30	0.030	0.054	0.027	0.062	0.162	0.284	0.242	0.139

先ほどの指摘通り、ページ1~4の値が0でない有限の値に収束しています。

断熱量子計算

ハミルトニアンとエネルギーギャップ

ハミルトニアン

アニーリング終状態のハミルトニアンを $h_1$ とします。すると

$\displaystyle{ h_1 = h(G) \equiv (\mathbb{1} - G)^\dagger (\mathbb{1} -G) }$

のようになります。ここで最終的に求めたいページランクベクトル ${\bf p}$ を思い出しましょう。 ${\bf p}$ はその導出方法から、 $G$ の固有値1の固有ベクトルであることがわかります。よって、求める終状態は $|\pi \rangle = {\bf p} / \| {\bf p} \|$ のように書くことができます。

同様の形で、アニーリング開始時のハミルトニアン $h_0$ を

$\displaystyle{ h_0 = h(G_c) \equiv (\mathbb{1} - G_c)^\dagger (\mathbb{1} -G_c) }$

のように定義します。ここで $G_c$ は先ほどのGoogle行列を全結合グラフにした場合のものです。この場合、全てのページ重要度が等しくなるはずなので、量子アニーリングの初期に準備する $h_0$ の基底状態は

$\displaystyle{ | \psi (0) \rangle = \sum_{j=1}^n \frac{|j \rangle}{\sqrt{n}} }$

となります。ここで $| j \rangle$ はページ $j$ がページ重要度1の状態です。

これらを用いて、量子アニーリングを行う際に用いるハミルトニアンは、時間発展を表す $s \in [0, 1$ ]を用いて

$\displaystyle{ h(s) = (1-s) h_0 + s h_1 }$

と書けます。

エネルギーギャップとアニーリング時間

Garnerone et al. 2012では、 $G$ を生成するモデルとしてBarabasi & Albert, 1999やBollobas et al., 2001の"Preferential attachment model"とKleinberg et al., 1999の"Copying model"の両方をインスタンスとして、エネルギーギャップをハイパフォーマンスコンピューティングで計算しました。その結果が以下の図です。

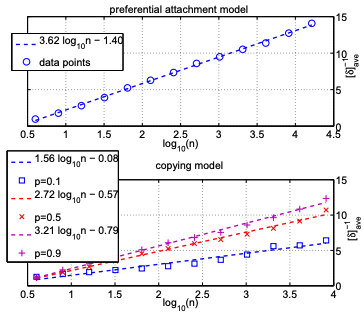
Relationship between the inverse of the energy gap and graph size — エネルギーギャップの逆数とグラフサイズの関係

縦軸にエネルギーギャップの逆数、横軸に $\log_{10} (n)$ としています。上図がPreferential attachment model, 下図がCopying modelでの結果です。この結果からエネルギーギャップが $\delta \propto 1/{\rm poly}(\log n)$ とわかります。このことと断熱定理より、求めたい終状態へ到達するためにかかるアニーリング時間は

$\displaystyle{ t_f \propto (\log n)^b \tag{1} }$

となります。ここで $b$ は小さい正の整数です。

古典と比べてどのくらい高速化したか？

この問題を解くときに、古典アルゴリズムで最速であるのはMarkov Chain Monte Carlo(MCMC)法です。この方法を用いるとページランクベクトルを算出するのにかかるステップ数は ${\mathcal O}[\log (n)$ ]であることが知られています。このアルゴリズムでは $\log n$ のランダムウォーカーが各ページから出発します(すなわち、総ウォーカー数は $n \log (n)$ )。各ステップ毎に隣あうページ間で情報のやりとりをするために ${\mathcal O} [\log (n)$ ]ビットが必要です。 ${\mathcal O}[\log (n)$ ]ステップ後に、各ページにウォーカーが何名訪れたかを計算することで、それがページランクとなります。よって古典アルゴリズムでこの問題を解くのに必要なコストは ${\mathcal O}[n \log (n)^2$ ]であることがわかります。
(1)式と比較すると、量子アニーリングによるページランクアルゴリズムの方が高速化されていることがわかります。

結言

日本人が生活する上で欠かせない技術となったGoogle検索、その背景にある検索エンジンのページランク付けアルゴリズムとそれを断熱量子計算で高速化できるということをご紹介しました。

参考文献

文責

中村翔、株式会社Jij
Sho K. NAKAMURA, Jij inc.
憂いの篩 -Pensieve-

※ 疑問点や間違いなどございましたら、お気軽にブログ上でご質問ください。

*1:可約グラフとは、可約行列が作るようなグラフのことです。可約行列は $\displaystyle{ P_2 (i, j) = \left( \begin{array}{cc} A & B \\ \bf{0} & C \end{array} \right) }$ のように、ある巨大な行列のなかに零行列が存在するようなものです。それに関連してある行列が作るグラフが強連結である時、その行列を既約行列(irreducible)と呼びます。既約でない行列を可約と呼びます。さらに補足すると、強連結とは以下のグラフのように任意の2点間に有向路が存在するようなグラフです。>