Jij Tech Blog

Jij inc.の開発日記です

平面超伝導プロセッサにおける非平面グラフ問題の量子近似最適化

量子ゲート 量子コンピュータ

この記事の概要

2020年4月にGoogle AI Quantum and CollaboratorsがarXivに投稿した論文 "Quantum Approximate Optimization of Non-Planar Graph Problems on a Planar Superconducting Processor" を読んだので、その理解を深めるためにアウトプットをしたものです。

序章: Sycamoreプロセッサ

Googleが開発した量子プロセッサです。超伝導量子ビットが54個搭載されています。

A picture of QPU Sycamore processor
A picture of QPU Sycamore processor

2019年10月23日にNatureから出版された論文"Quantum supremacy using a programmable superconducting processor"で、量子超越(Quantum supremacy)を達成したことが報告されました。その当時、世界最先端を行く古典スーパーコンピュータでおよそ10000年かかる計算を200秒ほどで完了させた、という驚きの成果を出したのがこのSycamoreプロセッサです。

序章: QAOA (Quantum Approximate Optimization Algorithms, 量子近似最適化アルゴリズム)

ここではQunaSysさんのQuantum Native Dojo, 5-3を元に、QAOAの概要を復習しましょう。

QAOA概要

量子アニーリングと同様に、組み合わせ最適化問題の解を求めるためのアルゴリズムです。NISQ上で実行できるとして、期待が寄せられています。

問題設定

QAOAでは z = z_1 z_2 \cdots z_n \ (z_i = 0, 1)というn桁のビット列zに関して、コスト関数 C(z) = \sum_\alpha C_\alpha (z)が最小になるようなzを探す問題を考えます。 C_\alpha(z)はビット列zを引数にとる何らかの関数で、ここでは特にイジングモデル的な C_\alpha(z) = z_i z_jというような項を考えれば良いでしょう。

この最小化問題を解くためにn qubitの量子系を用います。そして \beta = (\beta^{(1)}, \beta^{(2)}, \dots, \beta^{(p)})、 \gamma = (\gamma^{(1)}, \gamma^{(2)}, \dots, \gamma^{(p)})をパラメータとして、次のような量子状態を考えましょう。

\displaystyle{ \left| s \right\rangle = \left| + \right\rangle^{\otimes n} = \frac{1}{2^{n/2}} \sum_{z=0}^{2^n-1} \left| z \right\rangle \\ \left| \beta, \gamma \right\rangle = U_X (\beta^{(p)}) U_C (\gamma^{(p)}) \cdots U_X (\beta^{(1)}) U_C (\gamma^{(1)}) \left| s \right\rangle }

ここで \left| + \right\rangle = \frac{1}{\sqrt{2}} (\left| 0 \right\rangle + \left| 1 \right\rangle )はX演算子の固有状態 X \left| + \right\rangle = \left| + \right\rangleであり

\displaystyle{ U_C (\gamma^{(i)}) = e^{-i\gamma^{(i)} C(Z)} = \prod_\alpha e^{-i\gamma^{(i)} C_\alpha (Z)} \\ U_X (\beta^{(i)}) = e^{-i\beta^{(i)} \sum_{j=1}^n X_j} = \prod_{j=1}^n e^{-i\beta^{(i)} X_j} }

C(Z)というのはビット列を引数にとる関数C(z)の入力にパウリ演算子 Z_1 Z_2 \cdots Z_nと代入したものです。そして F(\beta, \gamma) = \langle \beta, \gamma |C(Z)| \beta, \gamma \rangleを最小にするような \beta, \gammaを探索することで、元々の最適化問題の答えを探そうとするのが、QAOAになります。

QAOAの手順

具体的なQAOAの定順は以下のようになります。

  1. 量子コンピュータ上で重ね合わせ状態 \left| s \right\rangle = \left| + \right\rangle^{\otimes n}を作成します。
  2. パラメータ \beta, \gammaに応じて、量子状態に U_C (\gamma^{(i)}), U_X (\beta^{(i)})を作用させていき、状態 \left| \beta, \gamma \right\rangleを得ます。
  3. 量子コンピュータを用いて \langle \beta, \gamma | C(Z)| \beta, \gamma \rangleを測定します。
  4. 古典コンピュータで \langle \beta, \gamma | C(Z)| \beta, \gamma \rangleがより小さくなるようにパラメータ \beta, \gammaをアップデートします。
  5. 1~4を繰り返し、最適な \beta^\ast, \gamma^\astを獲得します。
  6. 状態 | \beta^\ast, \gamma^\ast \rangleに対して、z方向の射影測定を複数回実行し、得られた(良さそうな)測定結果 z_1 \cdots z_nを元々の最適化問題の解として採用します(注意: 測定結果 z_1 \cdots z_nは古典ビットのことです)。

数値実験に用いた問題

コスト関数と対応する演算子

この論文では3つのグラフ問題を解いています。その全ての問題で、コスト関数に

\displaystyle{ C(z) = \sum_{j < k} w_{jk} z_j z_k }

を採用しています。 \omega_{jk} \in \{ 0, \pm 1 \}はエッジの重みを表すもので、 \omega_{jk} = 0ならば点 jと kが繋がっていないことを表しています。

これに対応する演算子として、ビット列 zをパウリ Zに置き換えた

\displaystyle{ C(Z) = \sum_{j < k} w_{jk} Z_j Z_k }

を用います。 Z_jは j番目の量子ビットにかかるパウリ Zです。

数値実験に用いたグラフ

Hardware Grid with a graph matching
Hardware grid with a graph matching
Hardware grid with a graph matching

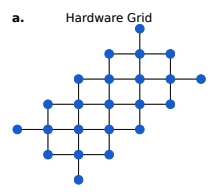
上図のような2次元正方格子において、最大で23量子ビットを用いてグラフマッチング問題を解きます。

Three-Regular Maxcut
Three-regular maxcut
Three-regular maxcut

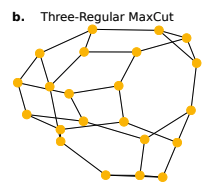
1つの点から3つに枝分かれするような、上図のグラフでMaxcut問題を解きます。用いているのは最大で22量子ビットです。

Sherrington-Kirkpatrick (SK) model
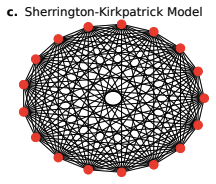
Fully connected graph with SK model
Fully connected graph with SK model

上図のような全結合グラフにおいて、SKモデルと呼ばれるスピングラスの理論モデルを解きます。最大で17量子ビットを用います。

コンパイルについて

今回の問題のコスト関数、もといそこから生まれるQAOAのためのユニタリ演算子$`U_C`$は

\displaystyle{ U_C (\gamma) = e^{-i \gamma C} = \prod_{j < k} e^{-i\gamma w_{jk} Z_j Z_k} }

となります。この演算を実装するために、この論文では以下のような量子回路を組んでいます。

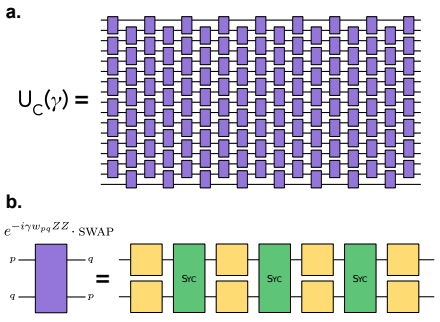
The linear swap network for a 17-qubit SK model
The linear swap network for a 17-qubit SK model

上図aは17量子ビットを用いてSKモデルを解くのに用いた量子回路図です。図のように e^{-i\gamma w_{jk} Z_jZ_k}演算を配置することで、 j < kを満たす全ての組み合わせを再現しています。

さらに e^{-i\gamma w_{pq} Z_p Z_q} \cdot {\rm SWAP}を上図bのように、黄色の \gamma \omega_{pq}に依存した1量子ビットの回転と緑色のSYCゲートで表現します。SYCゲートの定義は以下のようなものです。

\displaystyle{ {\rm SYC} = {\rm iSWAP}^\dagger \cdot {\rm CPHASE}(-\frac{\pi}{6}) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & -i & 0 \\ 0 & -i & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{-\frac{\pi}{6}i} \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & -i & 0 \\ 0 & -i & 0 & 0 \\ 0 & 0 & 0 & e^{-\frac{\pi}{6}i} \end{array} \right) }

エネルギーランドスケープと最適化されていく様子

以下に \beta \in [ -\pi/4, \pi/4 ], \gamma \in [ 0, \pi/2] におけるエネルギーランドスケープと、QAOAのイテレーションによりエネルギーが遷移していく様子を示します。

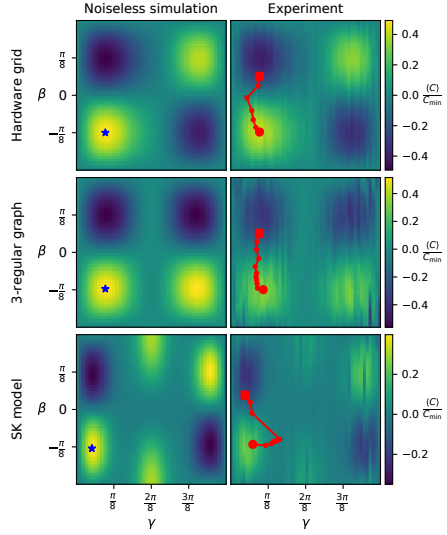
Landscape features and optimization trace
Landscape features and optimization trace

右列がシミュレーションによるエネルギーランドスケープで、図中の青星印は局所最適解の場所を示しています。右図はSycamoreの実験による量子回路の深さ( U_X U_Cを作用させる回数)が p=1のときのエネルギーランドスケープで、赤四角から始まる折れ線はQAOAによる最適解探索の様子を示しています。カラーコントアはコストを表しており、黄色がコストの低い部分、黒色がコストが高い部分に対応します。Hardware gridは23量子ビット、3-regular graphは14量子ビット、そしてSKモデルは11量子ビットのときの様子を示しています。
Sycamoreによる数値実験では、青星印の最適解に向かって状態が遷移していく様子がわかります。

QAOAにおけるSycamoreの性能

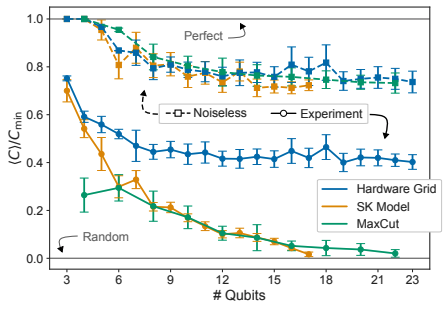
QAOA performance as a function of problem size n
QAOA performance as a function of problem size n

上図は p=3のとき、横軸を量子ビット数、縦軸をコストの小ささ(1は最適解、0はランダムな解)を表しています。実線がSycamoreの数値実験の結果です。Hardware grid問題は量子ビットの数に依存せず一定に落ち着いています。一方でMaxCutとSK Modelでは量子ビット数が増加するほど、ハードウェアのノイズによる影響を大きく受けています。

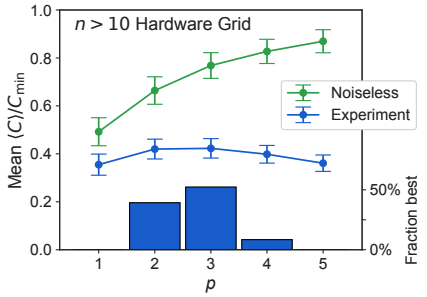
QAOA performance as a function of depth p
QAOA performance as a function of depth p

そして次の図は横軸を p、縦軸をHardware grid問題を解いたときの性能としたときのものです。緑線のシミュレーションは pを増やすごとに最適化されていきますが、Sycamoreによる数値実験ではむしろ精度が落ちています。下の棒グラフは各 pのとき、どのくらいのパーセンテージ最高のパフォーマンスを発揮できたかを表しています。 p=3が最高パフォーマンスを記録していることがわかります。

結言

Googleの量子プロセッサSycamoreによる数値実験の論文をご紹介しました。QAOAを実際に行った結果、現在のNISQデバイスでは p=3くらいの量子回路の深さが最良の結果を示しました。しかし今後のノイズ抑制技術次第では、この結果も大いに変わってくることでしょう。

参考文献

文責

中村翔、株式会社Jij
Sho K. NAKAMURA, Jij inc.
憂いの篩 -Pensieve-

※ 疑問点や間違いなどございましたら、お気軽にブログ上でご質問ください。