この記事の概要
2020年8月4日に投稿された、Rao et al. "Quantum amplitude estimation algorithms on IBM quantum devices"を読んだのでその理解を深めるためにアウトプットしたものです。
量子回路で数値積分する方法
演算子 と数値積分
と数値積分
こちらの記事の演算子を
に作用させます。このとき、求めたい状態
と求めたくない状態
が補助量子ビット
の前に現れます。しかしこの求めたい状態・求めたくない状態はこれまでの議論から直交している必要はなく、任意の状態を選んでよいことがわかります。よって
とします。ここで
です。すると
この状態で最後の番目の補助量子ビットを測定すると、
が測定される確率は
となります。ここでは
番目の分割領域を代表する
座標です。これは積分を離散化した以下の表式
において分割数をとしたものに等しいです。よってこれから数値積分が行えることがわかります。
量子回路
以下にを数値積分するための量子回路
を示します。
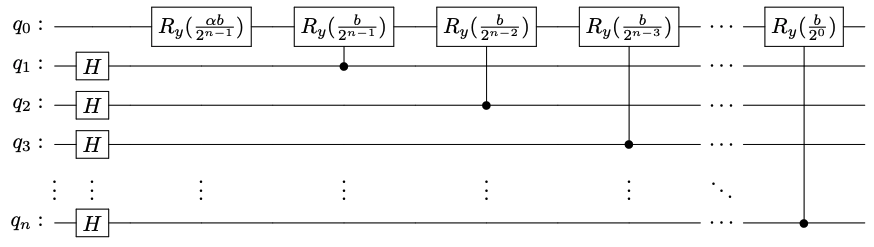
最初の一般位相ゲートに現れる
]は、各分割領域内のどの点を積分のための代表点とするかを表す定数です。例えば分割領域の左端の点を代表点とする場合は
、真ん中の点を代表点とする場合は
、そして右端の点を代表点とする場合は
とします。
具体例
下図のようにを
、分割数
、各分割における代表点を真ん中の点
として、積分することを考えましょう。
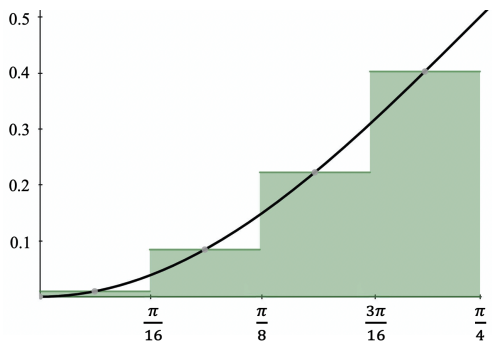
演算子を量子回路で表すと以下のようになります。
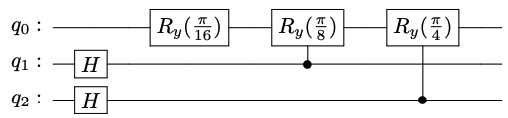
それではに演算子
を作用させましょう。
よって最後の補助量子ビット測定したときにを得る確率は
となります。これと実際に積分を離散化したもの
を比較すると、量子回路を用いた積分値はこれをで割ったものになっていることがわかります。
ここから精度を上げるためには?
分割数はより、1量子ビット増やすごとに積分範囲の分割数が2倍され、数値積分の精度が上がることがわかります。しかし、現状では限られた量子ビットの資源しか持ち合わせていないため、これを単純に数を増やすというのは困難です。
よってこの数値積分の精度を上げる手法として、測定を繰り返す手法 Iterative Quantum Amplitude Estimation, IQAE や異なる増幅回数の結果から最尤推定を用いる方法 Maximum Likelihood Quantum Amplitude Estimation, MLQAE などがあります。
この論文の主張
この論文ではIQAEとMLQAEによる数値積分をIBM Qに実装し、2つのどちらがより精度良く数値積分を求めることができるかを比較検証したものです。
2量子ビットでの実装
以下に2量子ビットで増幅演算子をQiskitで実装したときの図を示します。

左から順に,
,
,
,
となります。元論文とこの記事の表記を合わせると
となります。
MLQAE
MLQAEにおいて重要なパラメータであるを作用させる回数を表す数列には、最も精度良く計算できる等差数列的な増やし方(EIS)を採用します。すなわち
のような量子回路を選びます。
数値計算結果
2量子ビットの場合
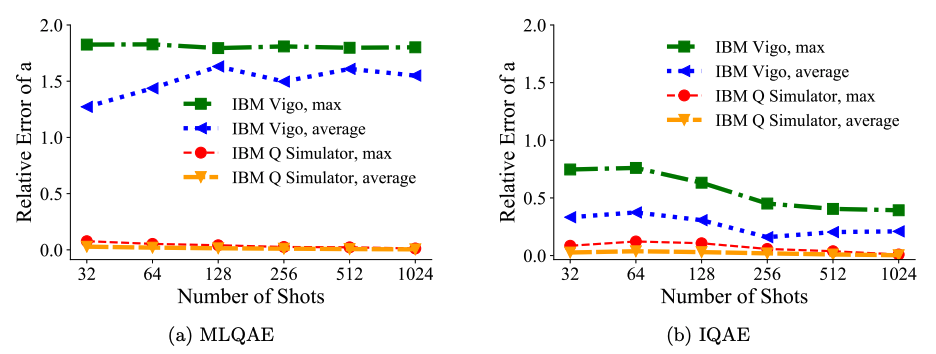
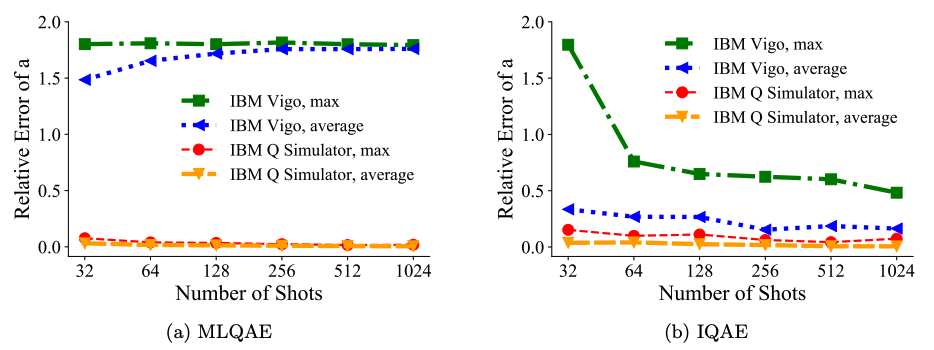
縦軸は真の値からのエラーの大きさ、横軸は測定回数です。上左図がMLQAE, そして上右図がIQAEの結果を表しています。Vigo, Q simulatorのどちらを見てもIQAEの方が精度良く数値計算を行えていることがわかります。
3量子ビットの場合
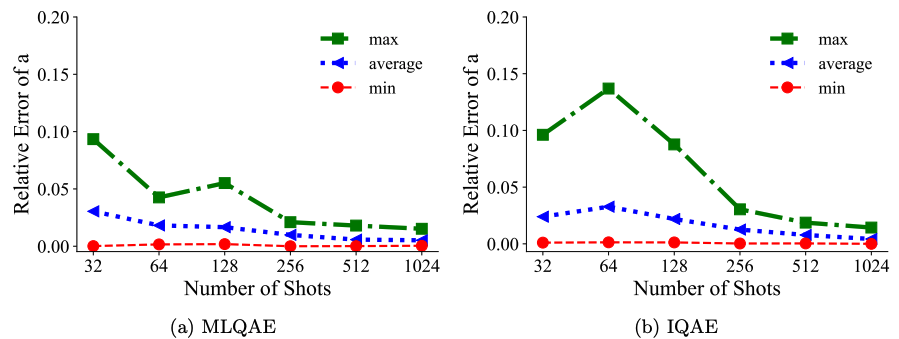
2量子ビットの場合と同じ図を、今度は3量子ビットでプロットしたものです。こちらもやはりIQAEの方が良い結果を出しています。
10量子ビットの場合
こちらはIBM Q simulatorのみの結果をプロットしています。
10量子ビットを用いた場合だと、どちらも同じくらいの精度が出ています。
考察: なぜMLQAEは精度が発揮できないのか
MLQAEで良い精度を出すための回路が深さを持ってしまうことに対して、IQAEは
をせいぜい4回も繰り返せばその精度を実現できるからであると主張しています。
結言
IQAE, MLQAEの2つの手法のどちらがNISQデバイスにおいて有効であるかを検証した論文をご紹介しました。この論文の主張では、同じ量子振幅推定であってもIQAEの方が良いという結果でした。