この記事の概要
2019年4月にarXivに投稿された論文のSuzuki et al. "Amplitude Estimation without Phase Estimation"を読み、その理解を深めるためにまとめたものです。
量子振幅増幅
詳しくはこちらの記事の量子振幅増幅
tech.j-ij.com
を参照してください。
最尤推定法による量子振幅推定
数式による説明
を測定回数(論文ではshotと表記)とします。そして
を測定したときに、求めたい状態
が測定された回数を
とします。すると求めたい状態が測定される確率は
より、尤度関数は
となります。するとに対する尤度関数は
となります。ここでです。最尤推定により、上述の
を最大化するような
が求めたい値となります。
図を用いた説明

上左図のように、増幅演算を様々な回数作用させた状態を測定しておきます。上真ん中図のようにそこから尤度関数
を計算します。それらを掛け合わせて、全体に対する尤度関数
を算出します。上右図のように、求めたい
の部分で
が最大となっているので、そこから値を求めます。
 の決定
の決定
論文ではクラメル・ラオの不等式とフィッシャー情報量を用いて、エラーの少ないを求めています。
- Linearly Incremental Sequence (LIS):
のように等差数列とする場合
- Exponentially Incremental Sequence (EIS):
のように等比数列とする場合
数値実験
以下の図は様々なに関して、横軸を
縦軸を真値からのエラーでプロットしたものです。
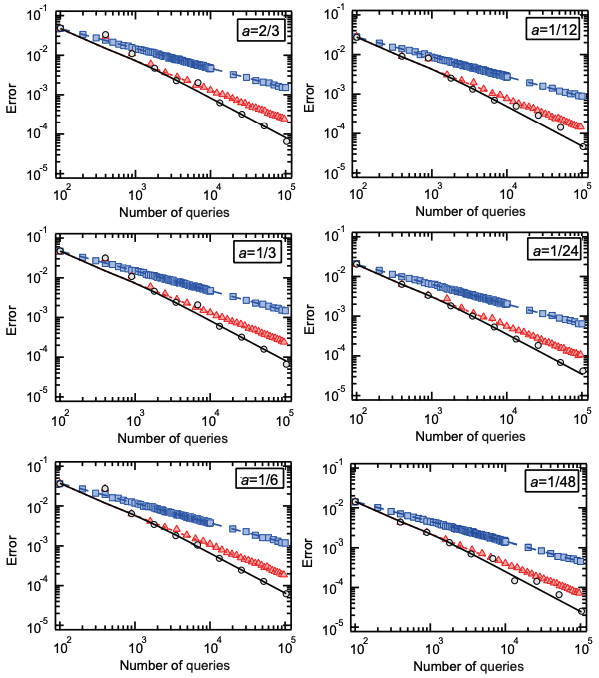
青四角はを古典的なランダムサンプリングした場合、赤三角は
をLISで決定した場合、そして黒丸はEISを採用した場合です。EISが最も精度良く振幅推定をできていることがわかります。
結言
量子位相推定を用いない量子振幅推定の方法として、最尤推定法を用いた手法をご紹介しました。さらに元論文ではこの手法をモンテカルロ積分へ応用することへ言及しています。