この記事の概要
Grinko et al. 2019, "Iterative Quantum Amplitude Estimation"を読んだので、その内容の理解を深めるためにアウトプットします。
量子位相推定 (Quantum Phase Estimation, QPE)
QunaSysさんのQuantum Native Dojo 2-4から、位相推定アルゴリズムは以下のような量子回路で記述されるのでした。
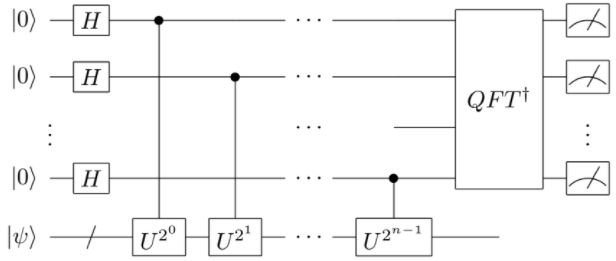
ここではアダマールゲート、
は測定用の各量子ビットを制御ビットとする制御ユニタリ演算、そして
は量子フーリエ逆変換をそれぞれ表します。固有値の位相情報を測定用の補助量子ビットに移した後で、量子フーリエ逆変換で位相を取り出すことが位相推定アルゴリズムです。
量子振幅推定 (Quantum Amplitude Estimation, QAE)
量子振幅増幅
演算子
まず求めたい量子ビットの状態
と、それ以外の求めたくない量子状態
とに分ける演算子を
とします。状態を分けるために補助量子ビットを一つ用いて、演算子
は
量子ビットに作用し
のように書かれます。ここで]は未知定数です。補助ビットの状態
に求めたい状態
の情報を移すことができました。以降、便宜上のため
と置きます。そして
として、これを初期に用意します。
解に対する位相反転演算子
次に解である状態の位相を反転させる演算子
を作用させます。ここではパウリの
演算子です。
初期状態を対称軸にした反転操作演算子
を作用させることで、初期状態を対称軸とした反転操作を行います。
ここで
より
k回繰り返し
これをを作用させることを
回繰り返すと
のようになります。
量子振幅推定とその量子回路
振幅増幅と同時に位相を補助量子ビットに移すことによって、振幅の推定を行います。これまでの議論を量子回路で表現すると以下のようになります。
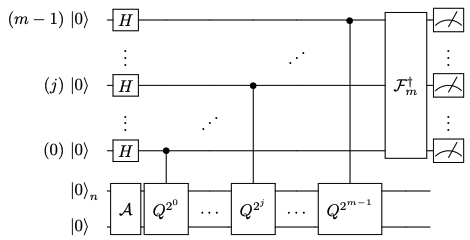
上図のように最後に量子フーリエ逆変換により位相推定を行えば、振幅の情報を取り出すことができます。
量子振幅推定の問題点
ここで議論してきた量子振幅推定では増幅演算の繰り返し回数を増やすごとに補助量子ビットを追加する必要があります。これではNISQデバイス上でこのアルゴリズムを実行するには限界があります。よって以下では、補助ビットの数が限られている場合に精度よく量子振幅推定を行うためのアルゴリズムIQAEをご紹介します。
反復法による量子振幅推定 (Iterative Quantum Amplitude Estimation, IQAE)
位相推定なしのQAE
これまでの議論から番目の量子ビットを測定すると、状態
が得られる確率は
となります。このの値と
が分かれば、求めたい
を得ることができます。
IQAEの考え方
最大となる
三角関数の公式から、
を推定することは
を推定することと同義です。
の値を推定するために、以下のように考えましょう。
の間に求めたい
があるとしましょう(
: lower,
: upperの意味)。今はcosの値を決定したいので、
は
]または
]の間にあると考えます。よって最大となる
を
が
または
の制限の元で探します。
IQAEアルゴリズム
以上の議論から、IQAEアルゴリズムは以下のようになります。
をFindNextK(
)という関数で更新します。
として
を更新します。
の間、1~2を繰り返します。
を計算し、値を返します。
最後に求まったから
とすれば、精度
が達成されます。
サブルーチン FindNextK
FindNextKはこのIQAEアルゴリズムの根幹をなす部分です。以下にその考え方を示します。
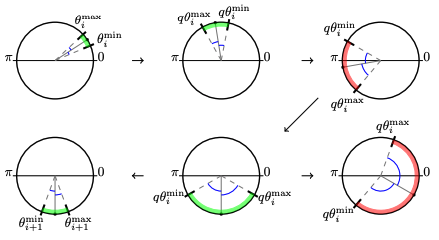
初期のインターバルを]として、それを
でスケールした
]を考えます。求めたいのは
を満たす
です。
上段左の図は初期の状態]です。ここに
をかけると、上段真ん中の図のようになります。
さらにの値を更新すると、上段右の図のようになります。しかしこれは
]または
]の間に両者が存在するという考えから外れてcosの値を一意に決定することができません。さらに値を更新し、下段真ん中図のようにします。ここからさらに
を更新すると下段右図のようになります。この状態もcosの値を一意に定めることができないので、FindNextKは下段真ん中図の
の値から
を出力します。
結果
このアルゴリズムとほかのアルゴリズムを比較するために、様々な(
を呼び出す回数)における測定結果(#)からのエラーをプロットしたものを以下に示します。
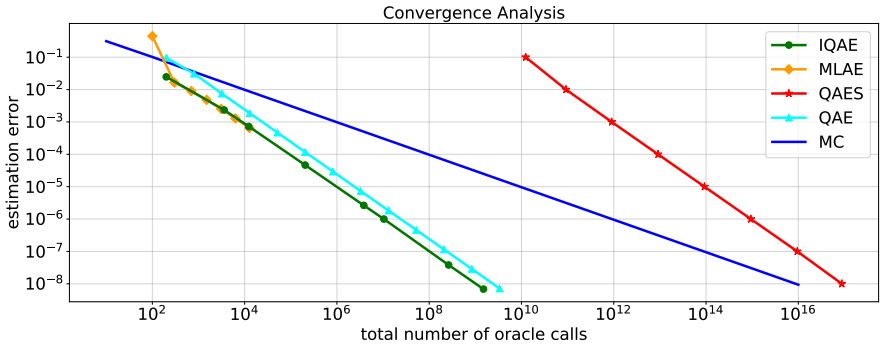
MLAE(Maximum Likelihood Amplitude Estimation)はIQAEと同じ傾向を示していますが、たくさんの補助量子ビットを必要とします。
結言
QPEを必要としないQAEアルゴリズムを紹介しました。こちらでは紹介してませんが、論文にはTheoremとして計算時間が2次高速化されることの証明も掲載されています。
またIBMのQiskitには、このIQAEが実装されています。
使用感を試してみるのも良いでしょう。
参考文献
- [1] https://arxiv.org/abs/1912.05559
- [2] 量子コンピュータを用いた高速数値積分
- [3] Quantum Native Dojoの位相推定(2-4)と量子探索アルゴリズム(8章)
- [4] Nielsen and Chuang "Quantum Computation and Quantum Information"